^^SIR model. Suscettibili, Infettivi, Recovered. Evoluzione.

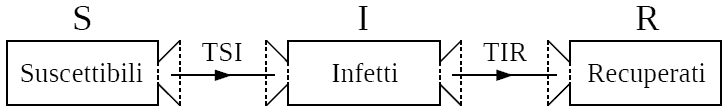
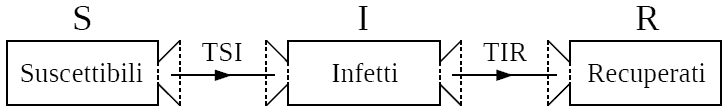
N ≡ popolazione totale

Lidea e'

1. calcolare i nuovi_infetti
2. calcolare i nuovi_guariti

in un intervallo di tempo ∆t.

Il risultato e'

Questo permette di calcolare la dinamica

Sn+1 = Sn + ∆S   dato S0 

In+1 = In + ∆S   dato I0

Rn+1 = Rn + ∆S   dato R0

Equazioni del modello in

Gli infetti diminuiscono se

nuovi_infetti < nuovi_guariti

βIS/N∆t < γI∆t

β/γ < N/S. Quando accade ?

S<N (Sensibili < Tutti)

matematica: 1<N/S, se β/γ < 1, allora β/γ < N/S

Epidemiologia:

S≈N all'inizio dell'epidemia se prima dell'apparizione dei primi infetti, tutti sono Sensibili all'infezione, poi per un po' rimane S≈N

β/γ < 1  garantisce il diminuire degli infetti da subito.

Dimostrazione  βIS/N∆t

una questione d'incontri.

Calcolare i nuovi infetti, in un intervallo di tempo ∆t

L'infezione e' dovuta all'incontro tra suscettibile e infettivo

• p probabilita' che l'incontro trasmetta l'infezione

non tutti gli incontri si concludono con un'infezione.

Quanti incontri ?

c∆t  nr medio di incontri di 1 persona nella durata ∆t

c  tasso di incontro

S/N  probabilita' di 1I o di 1R di incontrare  S

(S-1)/N  probabilita' di un S di incontrare S

per N grande arrotondiamo

S/N  probabilita' di 1 S I R di incontrare  S

I/N   probabilita' di 1 S I R di incontrare  I

R/N   probabilita' di 1 S I R di incontrare  R

Punto di vista dei sensibili

c∆tS  nr di incontri dei S nella durata ∆t,

I/N    e' la frazione di incontri con gli infettivi

p       e' la frazione di incontri che trasmette l'infezione

c∆tS*I/N*p  nr di nuovi infetti

Punto di vista degli infettivi

c∆tI   nr di incontri degli I nella durata ∆t,

S/N    e' la frazione di incontri con i suscettibili

p       e' la frazione di incontri che trasmette l'infezione

c∆tI*S/N*p  nr di nuovi infetti

In entrambi i punti di vista

pcSI/N∆t  nr di nuovi infetti

β≡pc

βSI/N∆t  nr di nuovi infetti

Approfondimento 2°

 

nr di incontri in una popolazione

c∆tN  nr di incontri nella popolazione di N individui nella durata ∆t.

Gli incontri simmetrici sono trascurabili.

Se tutti incontrassero tutti, gli incontri sarebbero n(n-1)/2, ma non e' il caso, poiche' il nr di incontri di ognuno e' molto minore della popolazione N

es:

1. se ognuno incontra 1 sola altra persona,
2. su una popolazione di N=1000,
3. e gli incontri sono a caso,

allora

1. la probabilita' di incontrare un prefissato individuo e' 1/(N-1)
2. la probabilita' che gli incontri di 2 coincidano e' 1/(N-1)²

Tipi di incontro

solo gli incontri SI sono potenzialmente infettivi

(S+I+R)/N = 1 

(S+I+R)/N * (S+I+R)/N  = 1*1 = 1

= (SS+SI+SR+IS+II+IR+RS+RI+RR)/N²

pc∆t  nr medio di infezioni prodotte da 1 infettivo nella durata ∆t

Fare il bilancio

per calcolare l'evoluzione della popolazione occorre fare il bilancio.

Bilancio di un "serbatoio", in generale

variazione popolazione =  (Entrate - Uscite) + (Nascite - Morti)

∆P = (E-U)+(N-M)

Casi importanti

Bilancio modello SIR

Ipotesi di bilancio del modello SIR: Nascite e Morti = 0

∆S= -US

∆I= EI-UI

∆R= ER

US = EI = TSI

UI = ER = TIR

TSI= βI(S/N)∆t

TIR= γI∆t

β costante, velocità di contagio unitaria
γ costante, velocità di guarigione unitaria

∆I= ∆S - ∆R

It's assumed that the permanence of each single subject in the epidemic states is a random variable with exponential distribution. More complex and realistic distributions (such as Erlang distribution) can be equally used with few modifications.

S+I+R=N = k

∆S+∆I+∆R = 0

∆S= -βI(S/N)∆t

∆R= γI∆t

∆I= ∆S - ∆R

Talk

S I R  indica la numerosita' delle popolazioni

S(t)  I(t)  R(t)   indica che la numerosita' dipende dal tempo

Di seguito

qui invece di pensare alla sequenza temporale di un individuo durante l'epidemia, si pensa ai gruppi-tipi di popolazione  Suscettibili Infetti Recuperati, a come varia lo loro numerosita' in funzione del tempo

Dirlo

Le epidemie si ripetono, sempre con lo stesso andamento, se la popolazione e' abbastanza grande; invece per una popolazione piccola, gli andamenti fluttuano.

Gli infetti diminuiscono se

c: via alla dimostrazione piu' complicata

∆I < 0 

∆I = βIS/N∆t - γI∆t  = (βS/N - γ)I∆t

β/γ < N/S ≈ 1   se S≈N  cioe' all'inizio dell'epidemia tutti sono Sensibili all'infezione.

β costante, velocità di contagio unitaria
γ costante, velocità di guarigione unitaria