^^Programma in formule. Classe 1.

Legenda

ym y medio

yp  y puntuale

yi y istantaneo

k costante

kprp costante d
proporzionalitā

inc incremento

 15 = 5*3
15
5 =
3
15
3 =
5
Prodotto, fattore, 2° fattore.

Prodotto, moltiplicando, moltiplicatore.

Leggere: 15 fratto 3
c = ab
c
a =
b
c
b =
a
idem
y = kx
y
k =
x
y
x =
k
idem
M = dmV
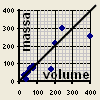
M
dm =
V
M
V =
dm
Massa, volume, densita' media.

Densita' media del corpo.
M = dV
M
d =
V
M
V =
d
Massa, volume, densita'.

Caso corpo omogeneo:

dm = dp = k ≡ d densita' della sostanza.
  P = PsmV
P
Psm =
V
P
V =
Psm
Peso, volume, peso specifico medio.

Peso specifico medio del corpo.

 
P = PsV
P
Ps =
V
P
V =
Ps
Peso, volume, peso specifico.

Caso corpo omogeneo:

Psm= Psp = k ≡ Ps della sostanza.
  F = kV
F
k =
V
M
V =
k
Forza di Archimede, volume immerso,

k costante di proporzionalita'.

k =  Ps del liquido
  F = pmA
F
pm =
A
F
A =
pm
Forza superficiale, area, pressione media.

Pressione media della forza distribuita sulla
superficie.
F = pA
F
p =
A
F
A =
p
Forza superficiale, area, pressione

Caso pressione uniforme:

pm = pp = k ≡ p.
  F = -kx
F
k = -
x
F
x = -
k
Forza elastica, allungamento,

costante elastica. Forza elastica, fatta dal

corpo e subita dall'ambiente.
  A = kN
A
k = 
N
A
N =
k
Forza di attrito, forza normale,
coefficiente di attrito.
Dinamica F = -kv
F
k = -
v
F
x = -
v
Forza viscosa, velocita', costante viscosa.

Caso moto laminare, non turbolento.
  F = ma
F
m =
a
F
a =
m
Forza risultante subita dal corpo,
accelerazione del corpo, massa d corpo.

2° Principio della dinamica di Newton.
  p = mv
p
m =
v
p
v =
m
Quantita' di moto del corpo (qm), massa e
velocita' del corpo.
  ∆p = fm∆t

∆p = f∆t

dp = fdt
∆p
fm =
∆t
∆p
∆t =
fm
Inc qm, durata, forza media nel tempo.

Forza media fm[t1;t2]; ∆p=p2-p1; ∆t=t2-t1

Caso fm = fi = k ≡ f, MFK: moto a f = k.
  P = Mg

 
P
g =
M
P
M =
g
Peso, massa, accelerazione di gravitā.

gT = acceleraz gravitā terrestre, a livello
del mare e 45° latitudine = 9,81 m/s2

  Ps = dg 
Ps
g =
d
Ps
d =
g
Peso specifico, densita', acceleraz di gravita'
  p = dgh
p
dg =
h
p
h =
dg
Pressione idrostatica, profondita', densita',
acceleraz gravita'
         
Geometria A = L2
A
1 =
L2
L = Ö(A) Area del quadrato in funzione del lato
  C = 2pR
C
2p =
R
C
R =
2p
Circonferenza in funzione del raggio.

C=kR    k = 2p
  A = pR2
A
p =
R2
C  
R = Ö(
)
2p  
Area cerchio in funzione del raggio

A=kR2   k = p 

Cinematica L = kN
L
k =
N
L
N =
k
Lunghezza s/av-volta, nr giri, kprp.

k = L1 lunghezza s/av-volta in 1 giro.
  L = kN
L
k =
N
L
N =
k
Lunghezza percorsa rotolando, nr giri, kprp.

k = L1 lunghezza percorsa in 1 giro
  ∆s = vm∆t
∆s
vm =
∆t
∆s
∆t =
vm
Spostamento, durata, velocita' media.

∆s = s2-s1 ;  ∆t = t2-t1

Velocita' media vm[t1;t2]
∆s = v∆t
∆s
v =
∆t
∆s
∆t =
v
Spostamento, durata, velocita'.

Caso vm = vi = k ≡ v, MVK: moto a v = k.

∆s = v∆t  legge oraria MVK
  ∆v = am∆t
∆v
am =
∆t
∆v
∆t =
am
Inc velocita', durata, acceleraz media

∆v = v2-v1 ;  ∆t = t2-t1

Acceleraz media am[t1;t2]
∆v = a∆t
∆v
a =
∆t
∆v
∆t =
a
Inc velocita', durata, acceleraz.

Caso am = ai = k ≡ a, MAK: moto ad a = k.

∆v = a∆t legge velocita'

  N=ft   t=TN

 

 
N   t
f=
   T=
t   N
N   t
t=
   N=
f   T
Nr cicli, durata, frequenza (media o k).
Durata, nr cicli, periodo.

fT=1   f=1/T   T=1/f    periodo e frequenza
  y=kx   x=hy

y=(1/h)x

x=(1/k)y
y   x
k=
   h=
x   y
y   x
x=
   y=
k   h
hk=1   h=1/k   k=1/h
y=f(x)  x y 
stato1 x1 y1
stato2 x2 y2
∆y = y'∆x
∆y
y'  =
∆x
∆y
∆x  =
y'
Rapporto incrementale d u funzione.

∆y = y2-y1 ;  ∆x = x2-x1
2 variabili
indipendenti.

Riducibili a una

 A = bh
A
b =
h
A
h =
b
Area di un rettangolo
  V = Abh
V
Ab =
h
V
h =
Ab
Volume di un cilindro, o di un parallelepipedo
  M = beF

   = bFe
M
b =
F
M
F =
b
Momento torcente (torchio di una forza),

braccio, forza.

be  braccio efficace, Fe forza efficace
  a = bR
a
b =
R
a
R =
b
a arco d circonferenza (o settore circolare);

b angolo sotteso, misurato in radianti;

R raggio della circonferenza (o settore).
Altri tipi di
formule		 x2 = x1+∆x 
y2 = y1+∆y
t2 = t1+∆t		 ∆x = x2-x1
∆y = y2-y1
∆t = t2-t1		 x1 = x2-∆x
y1 = y2-∆y
t1 = t2-∆t		 Incremento col segno, di una

grandezza variabile

y=∆y |y0=0; x=∆x |x0=0 ; t=∆t |t0=0

  B=A+s s=B-A A=B-s scarto, o errore assoluto, di B rispetto ad A
  B=A+A*sR sR=(B-A)/A A=B/(1+sR) scarto relativo
        scarto%    s% = sR*100%
    pA = pB   A,B superfici. Pressione uniforme e isotropa.
Principio di Pascal per i fluidi.
    ∑F = 0   Equilibrio delle forze.
    ∑M = 0   Equilibrio dei momenti.
    p1 = p2   Conservazione quantita' di moto
    FAB=-FBA

Maz-reaz=0

   3° Principio della dinamica.
         
         

 

 

 

 

Velocita' media vm[t1;t2]

= rapporto incrementale della

pos, nell'intervallo [t1;t2]
∆s s2-s1 s
vm=
 = 
 = 
∆t t2-t1 t
s e t equivoci: doppio significato.
s posizione e spazio percorso

t istante e tempo trascorso
Velocita' istantanea

= limite del

rapporto incrementale
    ∆s
vi =  limite 
  ∆t→0   ∆t
    s2-s1
vi[t1] =  limite 
  t2→t1   t2-t1
     
Acceleraz media am[t1;t2]

= rapporto incrementale della

velocitā, nell'intervallo [t1;t2]
 ∆v  v2-v1
am=
 = 
∆t t2-t1
v non si usa per indicare ∆v

(diversamente da s).
Accelerazione istantanea

= limite del

rapporto incrementale
    ∆v
ai =  limite 
  ∆t→0   ∆t
    v2-v1
ai[t1] =  limite 
  t2→t1   t2-t1

 

 

Rapporto
incrementale
di una funzione.
y=f(x)  x y 
stato1 x1 y1
stato2 x2 y2
∆y  y2-y1 
y' =
=
∆x x2-x1
∆y' y'2-y'1
y"=
=
∆x x2-x1
Velocita' di variaz
d u grandezza. 		∆y = y2-y1
∆t = t2-t1
∆y y2-y1
v ≡vy=
=
∆t t2-t1
∆vy v2-v1
a ≡ay=
=
∆t t2-t1
Fenomeni ciclici f=N(1 s)
T=t(1 ciclo)

 
N t
f =
    T =
t N
1 1
f*T=1    f =
   T =
T f
       

 

Titolo

Programma svolto, guardando alle formule. Classe 1.

Alter espo

 

  N = ft
N
f  =
t
N
t  =
f
Nr cicli, durata, frequenza.
  t = TN
t
T  =
N
t
N  =
T
Durata, nr cicli, periodo
  1 = fT
1
f  =
T
1
T  =
f
periodo e frequenza
  a = bR
a
b =
R
a
R =
b
a arco d circonferenza,

b angolo misurato in radianti.

Misura dell'arco rispetto al raggio.