Raffigurare
Le coppie di valori (VoLuMe ; MaSsA)
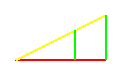
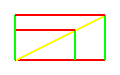
si possono raffigurare con un triangolo rettangolo, o un rettangolo, in cui :
VoLuMe=BaSe
e MaSsA=AlTeZzA.
(VoLuMe ; MaSsA)
= (BaSe ; AlTeZzA).




E' la forma usata in fisica, poiche' tramite la denominazione mette in evidenza come e' organizzato il sistema sotto studio: in sistemi e variabili.
|
Consideriamo 2 corpi. Di tutte le grandezze misurabili di un corpo, qui si considerano solo: VoLuMe e MaSsA - i valori di un corpo "piccolo": volume_piccolo e massa_piccola - e i valori dell'altro corpo "GRANDE": VOLUME_GRANDE e MASSA_GRANDE. |
|
|
In astratto, con le variabili astratte x e y:
|
 
|
RaffigurareLe coppie di valori (VoLuMe ; MaSsA)
si possono raffigurare con un triangolo rettangolo, o un rettangolo, in cui : |
    |
|
|
Rapporto tra i valori della grandezza omonimaviene interpretato come: |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
|
Rapporto tra i valori di grandezze dello stesso sistemaviene interpretato come: |
Il rapporto tra 2 i numeri di 2 misure esprime la misura di una grandezza rispetto all'altra, in altre parole: quanto una e' piu' grande dell'altra.
Pero' il rapporto si puo' interpretare anche in un altro modo:
quanto del primo termine corrisponde a 1 unita' del secondo termine.
| rapporto tra le variabili di 2 sistemi |
rapporto tra le variabili dello stesso sistema |
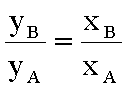 |
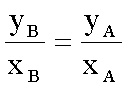 |