 |
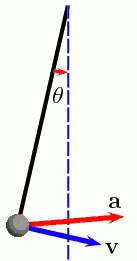
E' uguale a quella di una saponetta che scivola su una linea sagomata a circonferenza, poiche' traiettoria e forze sono uguali.
La forza della fune
La forza peso
Quindi per il moto 2D, ma ad 1 grado di liberta', e' determinato il campo di forze
| x | ascissa curvilinea, con origine nel punto piu' basso |
|---|---|
| L | lunghezza del pendolo |
| β = x/L | e' l'angolo espresso in radianti |
| mg | la forza peso |
mg*senβ e' la forza tangente alla traiettoria
| Equazione del moto (mista) | : m*x" = - mg*sen(β) |
| Equazione del moto (in x) | : m*x" = - mg*sen(x/L) |
| Equazione del moto (in β) | : m*L*β" = - mg*sen(β) |
Eq moto scritta rispetto alla variabile ascissa curvilinea, o all'angolo.
| g | ||
| β" + | sen(β) = 0 | |
| L |
e' la forma finale scelta poiche' e' la piu' vicina alla forma canonica delle eq differenziali.
| Standard approximation | senβ ≈ β e' senβ < β |
|---|---|
| Better approximation | senβ ≈ βcos(β/2) ≈ βcos(βM/2) |
| g | g | ||||||
| x" + | x = 0 | riconosco x"+ω2x=0 | ω2 = | ||||
| L | L |
|
L lunghezza del pendolo g accelerazione gravita' |
| g*cos(βM/2) | g*cos(βM/2) | ||||||
| x" + | x = 0 | riconosco x"+ω2x=0 | ω2 = | ||||
| L | L |
|
L lunghezza del pendolo g accelerazione gravita' |
| 1 | 1 | ||||
| TB = T* | e' | > 1 poiche' cos < 1 | |||
| √cos(βM/2) | √cos(βM/2) |
Come giustificare che il periodo e' piu' lungo ?
Seno approssimato, piccoli angoli.