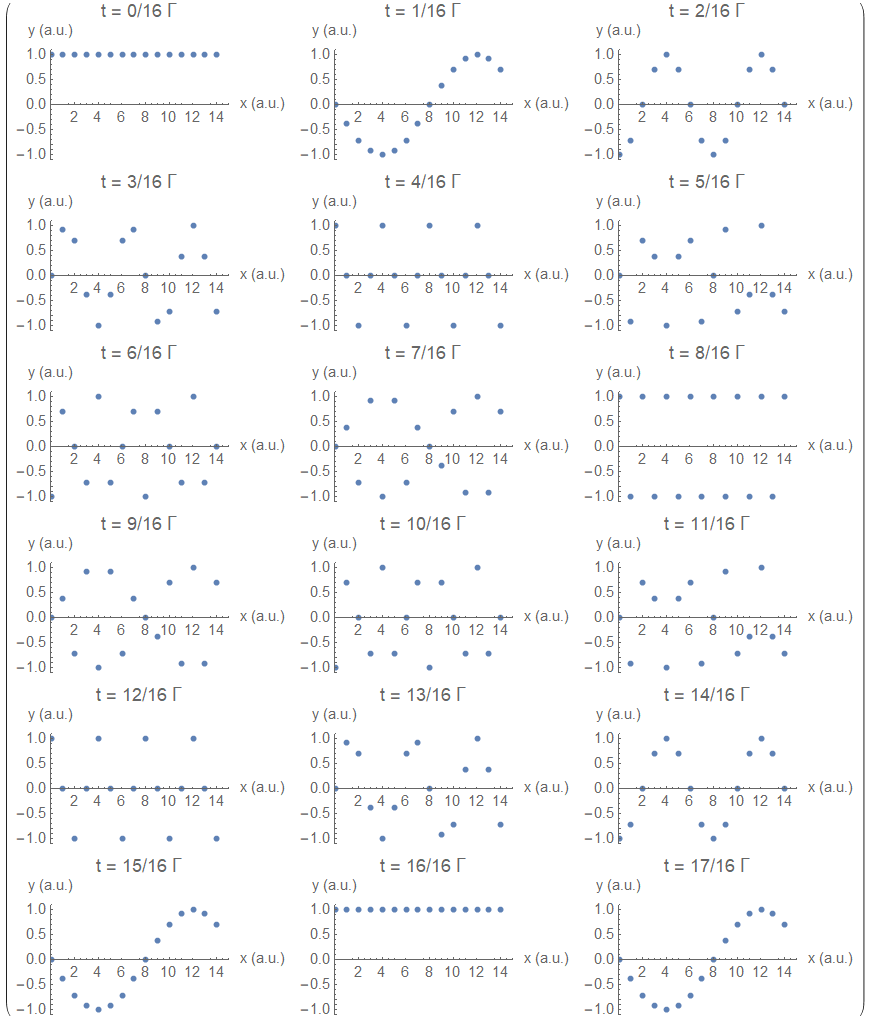
wp/Pendulum_wave e' una pagina neonata di Wikipedia (la incontro 17-8-2023), nasce 9-4-2023
ho ricevuto un
è un bel giochino, mi sono divertito a ripetere la simulazione descritta in uno degli articoli citati su wiki, v. lmg
In effetti, essendo i pendoli disaccoppiati, il sistema è facilmente prevedibile.
inizialmente ho fatto fatica a capire l'img poiche' i filmati visti mi facevano supporre la sfera oscillante piu' veloce a sx, le piu' lente a dx, invece qui e' il contrario. Cio' mi ha fatto riflettere anche sugli aspetti cognitivi.
Dall'ispezione complessiva, la mia comprensione finale e' riassunta da
| sfera | cicli(T) "frequenza" |
periodo sfera | cicli(T/2) | cicli(T/4) |
|---|---|---|---|---|
| 0 | 4 | 1/4 = 0,25 | 2 | 1 |
| 1 | 5 | 1/5 | 2,5 | 1,25 |
| 2 | 6 | 1/6 | 3 | 1,5 |
| 3 | 7 | 1/7 | 3,5 | 1,75 |
| 4 | 8 | 1/8 = 0,125 | 4 | 2 |
| 5 | 9 | 1/9 | 4,5 | 2,25 |
| 6 | 10 | 1/10 | 5 | 2,5 |
| 7 | 11 | 1/11 | 5,5 | 2,75 |
| 8 | 12 | 1/12 | 6 | 3 |
| 9 | 13 | 1/13 | 6,5 | 3,25 |
| 10 | 14 | 1/14 | 7 | 3,5 |
| 11 | 15 | 1/15 | 7,5 | 3,75 |
| 12 | 16 | 1/16 = 0,0625 | 8 | 4 |
| 13 | 17 | 1/17 | 8,5 | 4,25 |
| 14 | 18 | 1/18 | 9 | 4,5 |
Mi e' sembrato di fare "Reverse engineering".
nella sequenza stroboscopica
| sfera | cicli(T) frequenza |
|---|---|
| 0.5 | 4.5 |
| 1.5 | 5.5 |
| 2.5 | 6.5 |
| ecc... |
poi estremizzare infittendo con tutti i punti del continuo, associandoli al continuo delle frequenze.
Cio' rompe la periodicita' del sistema complessivo. Anche 2 soli punti con periodi incommensurabili non ripeteranno mai la configurazione iniziale.
Trovare la funzione che produce i dati per l'img ricevuta
f(x):= cos( 2π(4 + x)t ) riproduce i dati per gli interi assoluti.
Ho semplicemente graficato f(x) con i valori continui di x;
unito con una poligonale le sfere per visualizzare la figura complessiva
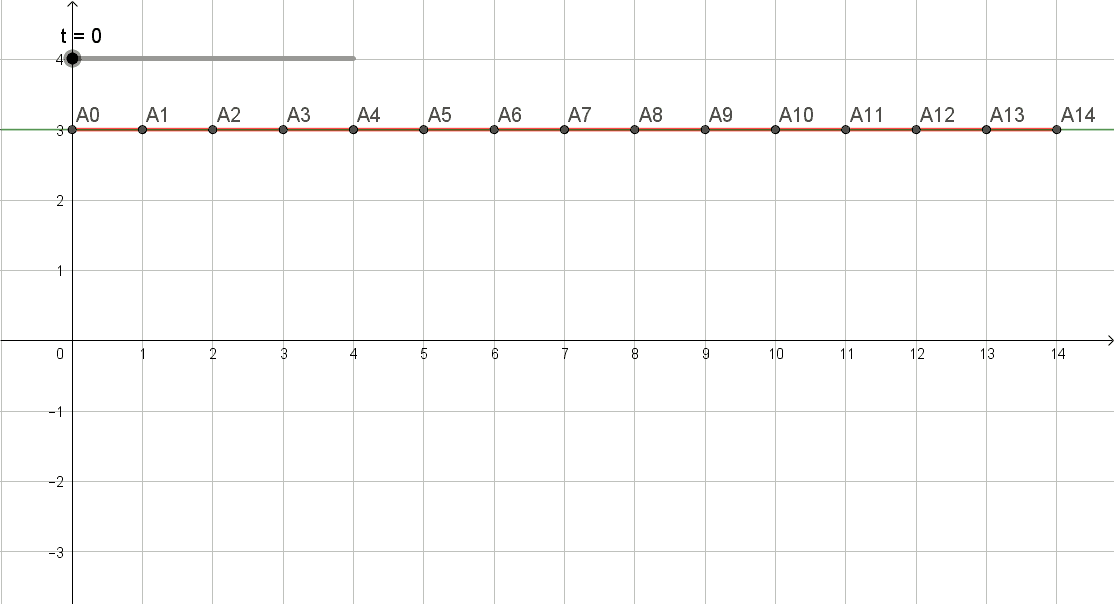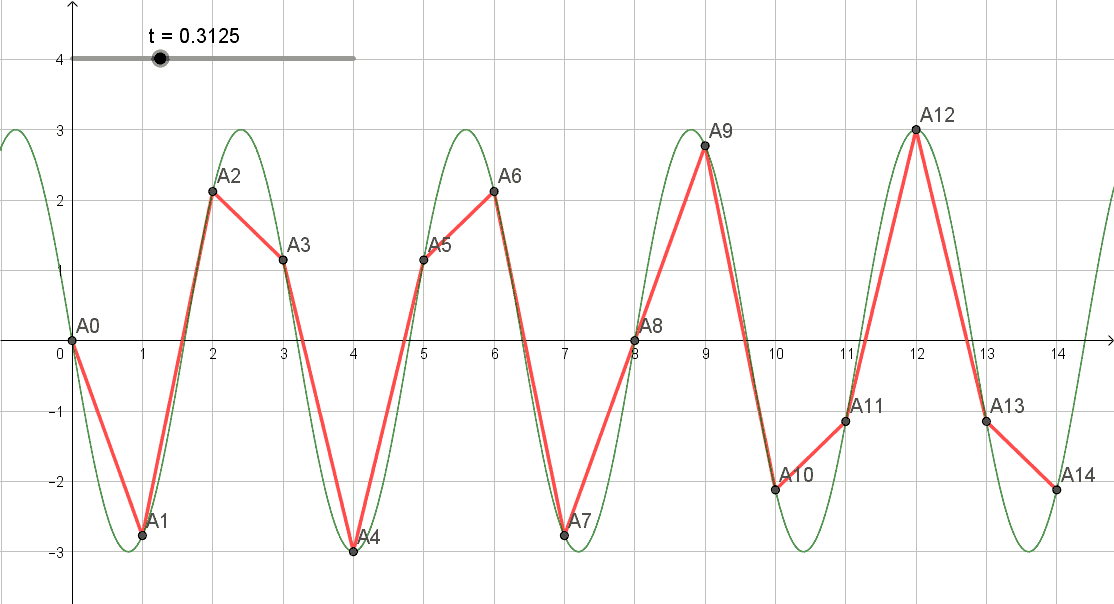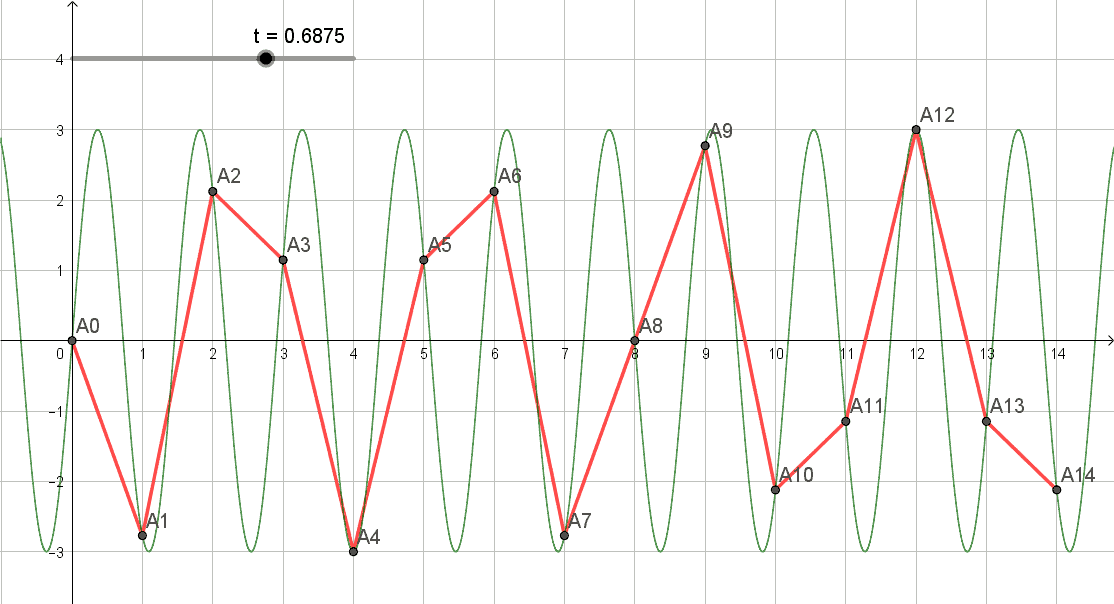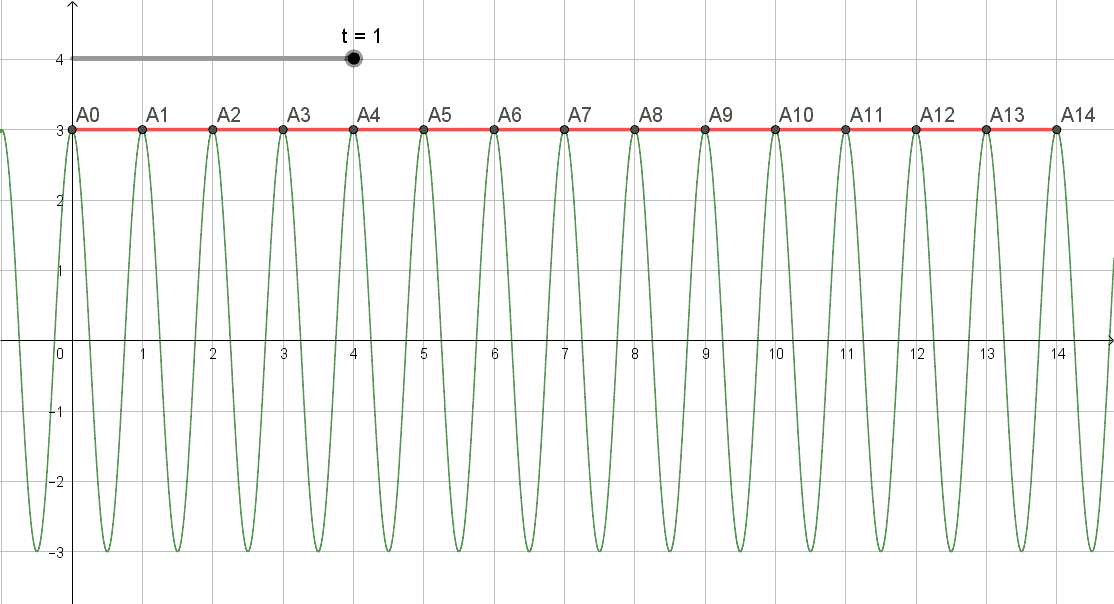
e' una gif prodotta da Geogebra col doc pend_wave_2.ggb.
Nell'ultimo frame il minimo delle valli e' posizionato sugli x seminteri 0.5 1.5 2.5 ecc... , la' dove il punto sovrastante della curva variabile ha oscillato con periodo 4.5 5.5 6.5 ecc...
ho aumentato il frame_rate per mostrare come si forma la sinusoide del frame1 al tempo 1/16T, che ho diviso in 25 parti
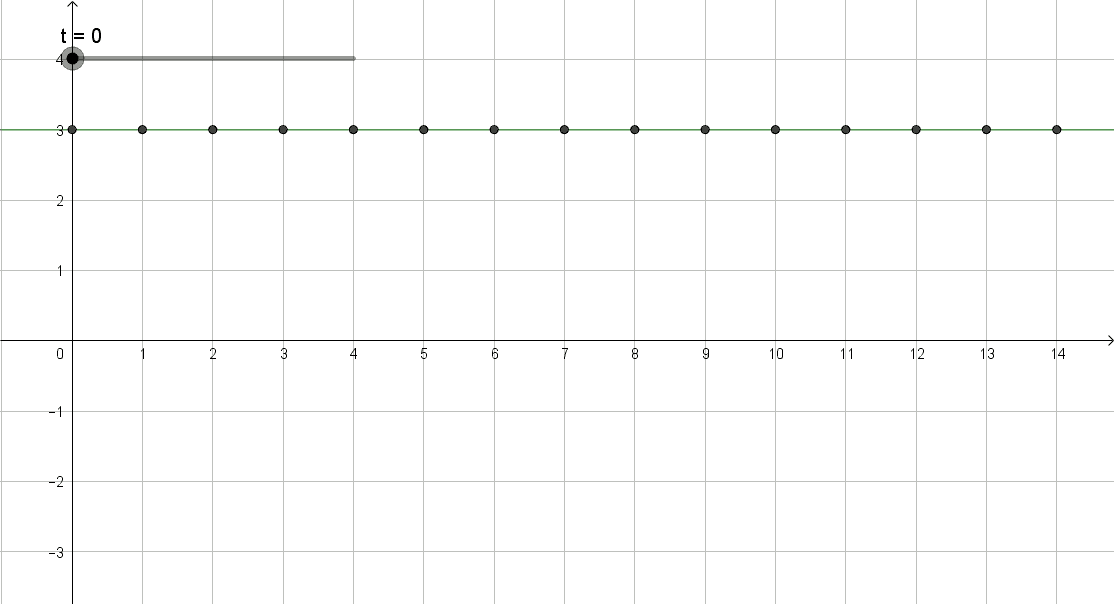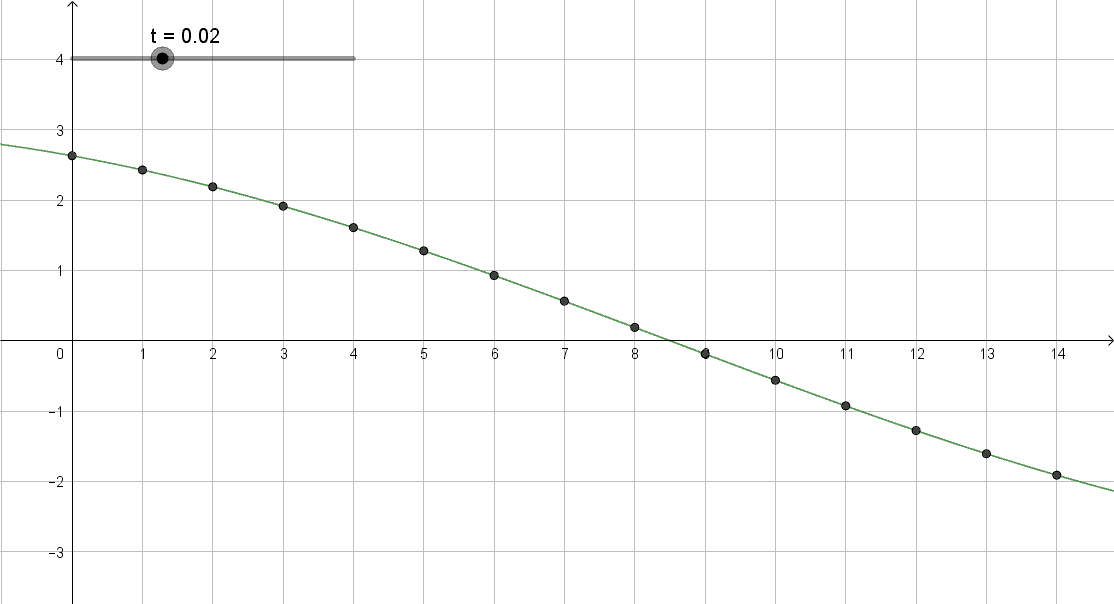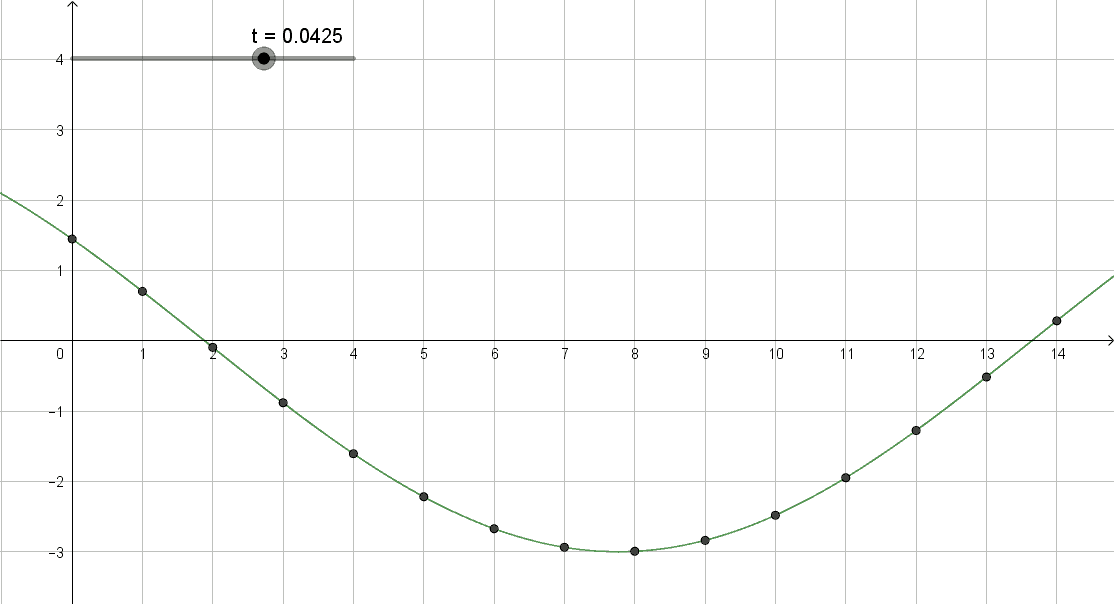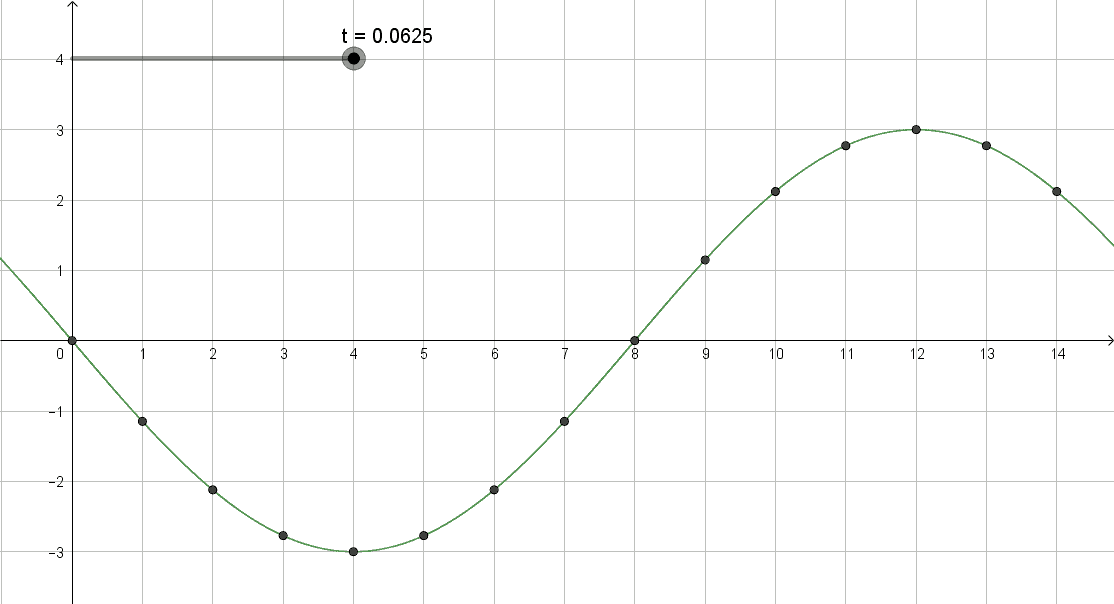
e' una gif prodotta da Geogebra col doc pend_wave_2b.ggb
Questa animazione ha raccordato la mia percezione dell'img strobo coi video visti in passato, era lo stesso comportamento presentanto con una prospettiva inizialmente irriconoscibile alla mia percezione, la ragione ha soccorso.
e che ha stimolato ulteriori osservazioni.
Lo slider che funge da tempo, quando in focus (basta clic sopra), e' comodo da muovere con i tasti freccia.
Ho scritto anche pend_wave_3.ggb che aumenta le sfere fino a sfera24; suggerisce relazioni tra ciclicita'.
Lo sfondo del grafico e' trascinabile (se in focus, basta clic sopra).
Trascinando lo sfondo del grafico a dx si scopre cosa accade per x= -1, -2, -3,
-4 (e oltre?).
Windows GeoGebra Classic 5.0.680 8-12-2021.
Oggi si scarica la versione 5.2.807 17-10-2023;
sul mio computer la nuova versione presenta lo stesso documento ingrandito del 50%, cio' implica che devo ridimensionarlo per vedere il campo visibile con la vecchia versione.