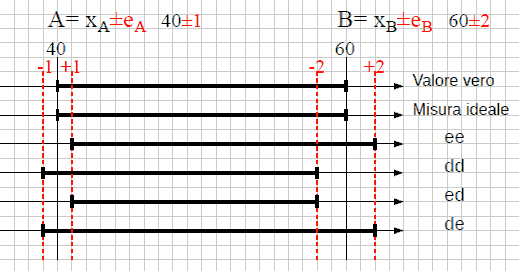
D ≡ B-A = (cB-cA) ± (eB+eA)
D ≡ B-A = 60±2 - 40±1 = 20±3
eB-A = eB+eA
L'errore assoluto della somma, e della differenza, e' uguale alla somma degli errori dei termini.
cioe': Quant'e' l'errore del risultato ottenuto tramite la differenza?
| E(a-b)= E(a) + E(b) | l'errore della differenza e' uguale alla somma degli errori degli operandi. |

D ≡ B-A = (cB-cA) ± (eB+eA) D ≡ B-A = 60±2 - 40±1 = 20±3 eB-A = eB+eA
L'errore assoluto della somma, e della differenza, e' uguale alla somma degli errori dei termini.
|
Lo discutiamo in modo significativo nel caso del calcolo-misura del volume per differenza.
lab approfondimento: Sostenere un peso con dinamometro e bilancia
contemporaneamente.
In classe: che deve recuperare i compiti in classe, preparazione per il
recupero
Lab: 1) 2 pulegge coassiali solidali di diametro una il doppi dell'altra.. 2) sollevae con l'ansa di una fune. 3) discesa di un volano sul perno e sul volano. 4) Pendolo interrotto.
https://phet.colorado.edu/sims/html/graphing-quadratics/latest/graphing-quadratics_en.html
Distanza su un asse cartesiano.
Asse cartesiano come riferimento spaziale.
Posizione di un punto su una linea ...
segmento calcolato come differenza dei segmenti_posizione dei suoi estremi
misurare la lunghezza di un intervallo
misurare la lunghezza dell'intervallo tra 2 punti sull'asse numerico
|
|
facendo tramite con come |
la
la la |
differenza della loro posizione differenza della loro posizione differenza della loro posizione differenza della loro posizione |
Posizione relativa. E' il raggruppamento degli argomenti.
Misurare il volume di un solido tramite il sistema di immersione in un liquido contenuto in un recipiente graduato. >>>
La misura finale voluta, si ottiene tramite una differenza.
| volume totale | VT = | 200 cm3 |
| volume liquido | VL = | 150 cm3 |
| volume solido | VS = VT - VL | 200-150= 50 |
| valore col massimo errore per | ||||
|---|---|---|---|---|
| E= 1 | difetto | eccesso | ||
| volume totale | VT = | 200 | 199 | 201 |
| volume liquido | VL = | 150 | 149 | 151 |
| volume solido | VS = VT - VL | 200-150 = 50 |
48 | 52 |
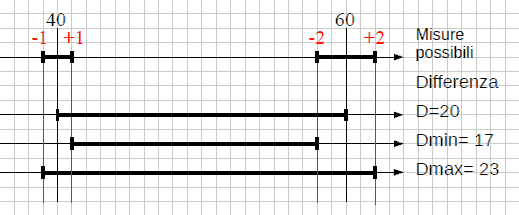
il valore della differenza non e' univoco, poiche' i termini dell'operazione sono variabili, e di conseguenza il risultato. Pero' questa variabilita' ha un limite di variazione, dato dal valore massimo e minimo ottenibili.
| Massimo | 201 - 149 = 52
max(max) - min(min) |
il massimo del maggiore, meno il minimo del minore
|
| Minimo | 199 - 151 = 48
min(max) - max(min) |
il minimo del maggiore, meno il massimo del minore |
| Massimo | 201 - 149 = 52
max(maggior) - min(minor)
|
|
| Minimo | 199 - 151 = 48
min(maggiori) - max(minori)
|
|
misurare la lunghezza dell'intervallo tra 2 punti sull'asse numerico
|
|
facendo tramite con come |
la
la la |
differenza della loro posizione differenza della loro posizione differenza della loro posizione differenza della loro posizione |
misurare la lunghezza dell'intervallo tra 2 punti sull'asse numerico
misurare la lunghezza dell'intervallo tra 2 punti sull'asse numerico
|
|
facendo la tramite la con la come |
differenza della loro posizione differenza della loro posizione differenza della loro posizione differenza della loro posizione |
misurare la lunghezza dell'intervallo tra 2 punti sull'asse numerico
|
|
facendo tramite |
la
la la |
differenza della loro posizione differenza della loro posizione differenza della loro posizione differenza della loro posizione |
D ≡ B-A = (cB - cA) ± (eB+eA)
D ≡ B-A = 60±2 - 40±1 = 20±3
e(B-A) = eB+eA

D ≡ B-A = (xB-xA) ± (eB+eA) D ≡ B-A = 60±2 - 40±1 = 20±3 eB-A = eB+eA
L'errore assoluto della somma, e della differenza, e' uguale alla somma degli errori dei termini.
|
|
D ≡ B-A = (xB-xA) ± (eA+eB)
D ≡ B-A = xB±eB - xA±eA = (xB-xA) ± (eA+eB)
D ≡ B-A = 60±2 - 40±1 = 20±3
D ≡ B-A = (60-40) ± (2+1) = 20±3
D ≡ B-A = (xB-xA) ± (eB+eA) D ≡ B-A = (60-40) ± (2+1) = 20±3
|
Quale delle versioni e' meglio ?
Si possono fare le combinazioni. Quelle in cui la formula numerica traduce esattamente quella letterale, sembrano pesanti.
zoom 66,7%

alla fine ho preferito img senza le scritte (formule) sotto, e ho fatto bene, poiche' le ho cambiate piu' volte.
Questa e' stata la prima versione, ma poi ho cominciato a cambiare la scritta sotto, e cio' mi ha portato a tagliarla dalla figura.
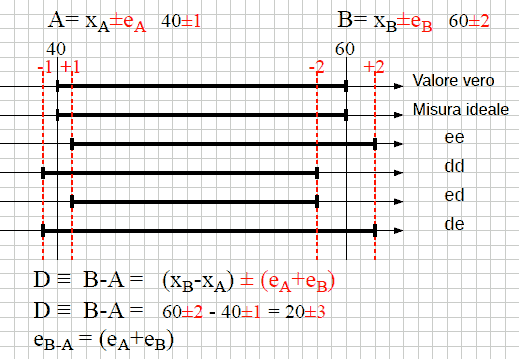

D ≡ B-A = (xB-xA) ± (eB+eA) D ≡ B-A = 60±2 - 40±1 = 20±3 eB-A = eB+eA
L'errore assoluto della somma, e della differenza, e' uguale alla somma degli errori dei termini.
|
| E= 1 cm3 | valore col massimo errore per | ||
| volume di acqua | VA = 120 cm3 | 119 cm3 | difetto |
| 121 cm3 | eccesso | ||
| volume totale | VT = 208 cm3 | 207 cm3 | difetto |
| 209 cm3 | eccesso |