^^Σ k³ = (Σ k)²   Serie dei cubi = quadrato serie aritmetica.

Σ k³ = (Σ k)²

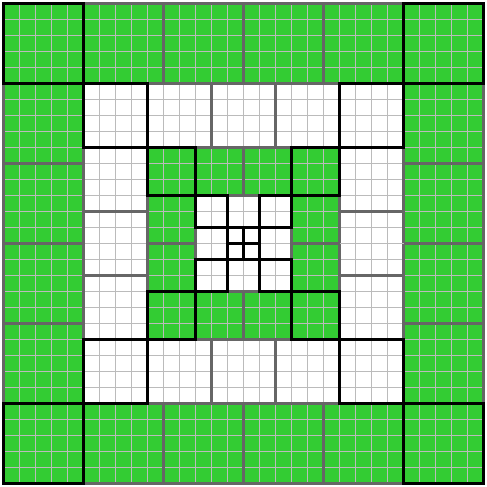
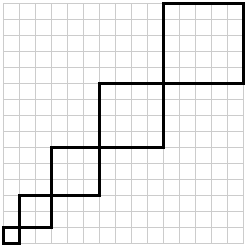
1³+2³+...+n³  =  (1+2+...+n)²

e' il teorema di Nicomachus wp

proof without words

Approfond

Come arrivarci ? (senza servirla a freddo)

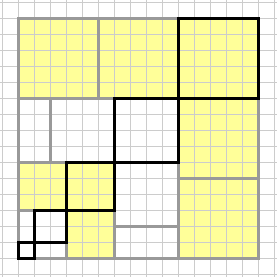
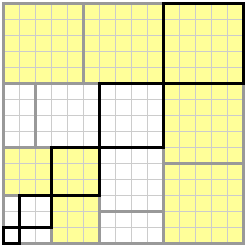
questa e' una figura che ho fatto spontaneamente in un altro contesto Rettangolo combinazione di segmenti

avrei poi dovuto artisticamente fare

e credo di averlo fatto o visto, ma poi non ho concluso

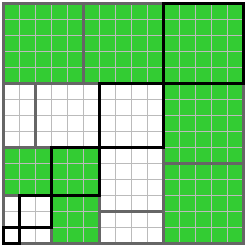
Un altro disegno che spontaneamente credo di aver fatto,

forse aggiunto il quadrato esterno

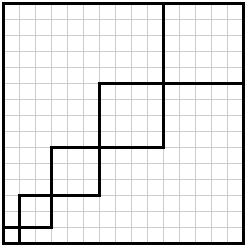
ma non credo gli altri quadrati

e poi non ho concluso

Verifica per alcuni casi n=2 3 4

1+2³ = (1+2)²                         1+8=3²   9=9

1+2³+3³ = (1+2+3)²               1+8+27=6²    36=36

1+2³+3³+4³ = (1+2+3+4)²    1+8+27+64=10²    100=100

dim letterale

(1+2+...+n)² = ((1+2+...+n-1)+n)²

=  (1+2+...+n-1)² + n² + 2n(1+2+...+n-1)

=  (1+2+...+n-1)² + n² + 2n(n²-n)/2

=  (1+2+...+n-1)² + n² +n³-n²

=  (1+2+...+n-1)² +n³

con questi passaggi si perde il paragone geometrico.

Per paragonare occorre pensare al paragone del quadrato

=  (1+2+...+n-1)² + n² + 2n(n(n-1)/2)

=  (1+2+...+n-1)² + n² + n²(n-1)

=  (1+2+...+n-1)² + n²n

es nr

(1+2+3+4)² =  ((1+2+3)+4)² = (1+2+3)² + 4² +2*4*(1+2+3) = 36+16+48 = 100

Σ k³ = (Σ k)²    Aryabhata is famous for the identity

Mi ha fatto ripensare alla serie aritmetica

distinguendo il caso pari dal dispari, che nella dimostrazione usuale del "raddoppio" si evita e quindi si perde.

Si potrebbe trasportare a questo caso facendo il doppio su entrambi gli assi, quindi moltiplicando per 4 i quadrati.

n(n+1)/2 =  (n/2)(n+1)  n pari

n(n+1)/2 =  ((n+1)/2) (n+1)  - (n+1)/2     n dispari

               =  ((n-1)/2) (n+1)  + (n+1)/2

yt/Olivier Pierre - Comment illustrer des calculs de sommes d'entiers ?

Talk

Dis .xcf | 2.xcf

Con cornice