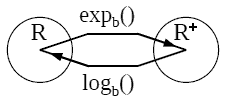
- funzione logaritmo
- funzione esponenziale inversa
- logb() logaritmo in base b
- fun inversa di expb()
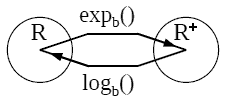
|
 |
Il logaritmo in base b
e' la funzione inversa dell'esponenziale in base b.
Detto coi valori della variabile
se y= expb(x) allora logb(y) = x
∀x logb(expb(x)) = x definizione la piu' sintetica.
La composizione di funzioni e' "commutativa"
∀x expb(logb(x)) = x
expb()logb() |
I = expb(logb()) = logb(expb(x)) |
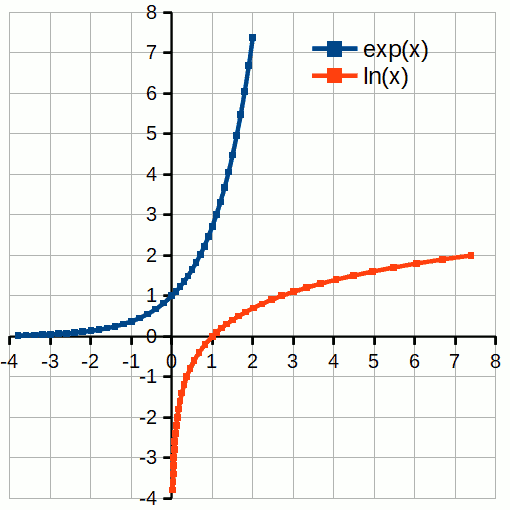
esponenziale e logaritmo sono funzioni inverse una dell'altra.
Come genesi, l'esponenziale e' prioritaria, e' la genitrice, ma poi nell'uso sono paritarie.
quando e' implicito quale sia la base, si omette di indicarla.
Normalmente la si omette nel caso che la base sia e.
ax=b ricavare x, l'incognita e' all'esponente
ax=b ∀a∈ℝ+≠1, ∀b∈ℝ+ ∃x∈ℝ: ax=b
questa e' la suriettivitą della funzione esponenziale exp:R→R+ .
ax= b x= loga(b)
Per linearitą di notazione, conviene introdurre.
y = bx ≡ expb(x) esponenziale di x in base b
cosi' come
la funzione radice e' l'inversa della funzione potenza.
| log(ex) = x | il logaritmo e' la funzione inversa dell'esponenziale |
| elog(x) = x | da cui l'esponenziale e' la funzione inversa del logaritmo |