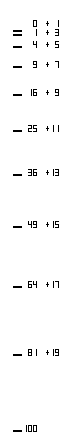| 120 |
Gli spostamenti lungo una linea e la loro composizione si possono numerizzare |
2
|
5
|
|
|
tramite i numeri relativi e la loro somma.
|
2
|
|
|
Se hanno verso opposto, numericamente
hanno segno opposto. |
1 |
|
|
|
|
|
| 900 |
In fisica il tempo e' raffigurato tramite la
linea del tempo. |
1 |
3 |
|
|
Segno-significato:
punto-istante, segmento-durata |
2 |
|
|
|
|
|
|
|
In linguaggio comune si usa dire "momento", in fisica puo'
significare 2 cose:
|
|
2
|
|
|
un istante, una durata breve
|
|
|
|
|
|
|
|
|
(Tempo) una durata breve, cosi' come (Spazio) una
lunghezza corta,
|
1
|
3
|
|
|
hanno un significato relativo.
|
1
|
|
|
|
es: un giorno e' breve relativamente ad un anno e lungo
rispetto a un minuto
|
1
|
|
|
|
|
|
|
|
Confronto: velocita' media, velocita' istantanea. Confronto delle
definizioni (in pratica).
|
|
5
|
|
- uguale: stessa formula |
2 |
|
|
- diverso: per la velocita' istantanea, in pratica si usa la durata
|
3 |
|
|
|
piu' breve che si
riesce col sistema di misura disponibile
|
|
|
|
|
|
|
|
|
Principio di continuita' della velocita'. Diminuendo l'intervallo
temporale di osservazione
|
|
2
|
|
la velocita' varia di meno. |
2 |
|
|
|
|
|
|
|
Confronto: velocita' scalare, vel vettoriale. Nel moto circolare
uniforme
|
1
|
3
|
|
|
la velocita' scalare e' costante
invece la velocita' vettoriale varia
|
2
|
|
|
|
|
|
|
|
La legge oraria del moto uniforme. Formula: s= v*t
|
1
|
6
|
|
|
Legenda: - s, t variabili correlate
|
1
|
|
|
|
- v velocita' costante
|
1
|
|
|
|
A parole: lo spazio percorso e' direttamente porporzionale
al tempo trascorso
|
3
|
|
|
|
|
|
|
|
|
|
|
| Esempio e spiegazione del moto ad accelerazione costante di
Galileo Galilei |
|
18 |
|
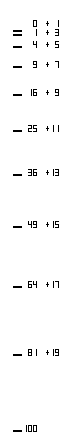
|
| A |
B
|
C |
D |
| t |
x
|
Dx |
D(Dx) |
| 0 |
0 = 02 |
+1 |
+2 |
| 1 |
1 = 12 |
+3 |
+2 |
| 2 |
4 =
22 |
+5 |
+2 |
| 3 |
9 = 32 |
+7 |
+2 |
| 4 |
16 = 42 |
+9 |
+2 |
| 5 |
25 = 52 |
+11 |
+2 |
| 6 |
36 = 62 |
+13 |
+2 |
| 7 |
49 = 72 |
+15 |
+2 |
| 8 |
64 = 82 |
+17 |
+2 |
| 9 |
81 =
92 |
+19 |
|
| 10 |
100 = 102 |
|
|
Nota: le tracce del moto vanno
disegnate in mm durante il cc.
Punti: 3 i numeri + 1 intestaz
Disegno: 2 punti.
|
- B: spazio-lunghezza percorsa |
1 |
|
| o spostamento dall'origine |
1 |
|
| dato da: dai quadrati dei
numeri interi |
1 |
|
| a partire da 0 |
1 |
|
| |
|
|
| - C: spostamenti consecutivi |
2 |
|
| dato da: dai
numeri dispari |
1 |
|
| |
|
|
| - D: variazioni degli spostamenti |
2 |
|
| |
|
|
| dato da: dal valore costante +2 |
1 |
|
| |
|
|
| |
|
|
| Condizioni iniziali: velocita' iniziale = 0 |
2 |
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
|
|
|
|
|
300
|
La variazione di una variabile e' anch'essa una variabile.
|
|
2
|
|
|
|
|
|
|
Questo modello del moto ad acceleraz=k e' piu' semplice di quello completo
poiche':
|
|
3
|
|
|
- guarda solo alle variazioni
|
1
|
|
|
|
- piuttosto che alle velocita' di variazione
|
2
|
|
|
|
|
|
|
|
L'esempio solito di fenomeno ciclico in fisica e' il moto
circolare uniforme.
|
|
2
|
|
|
|
|
|
|
Osserviamo il fenomeno ciclico per N cicli per una durata complessiva
t.
|
|
9
|
|
|
frequenza f= N/t numero di cicli in 1 unita'
di tempo
|
3
|
|
|
|
periodo T = t/N durata di 1 ciclo
|
3
|
|
|
|
Relazione tra frequenza e periodo: f*T=1 f=1/T
T=1/f
|
3
|
|
|
|
|
|
|
200
|
p4
|
- v = velocita' del moto di un punto mobile
|
2
|
14
|
|
|
- Dx variazione di posizione del moto
|
2
|
|
|
|
- Dt variazione di tempo del moto
|
2
|
|
|
|
- x1 posizione iniziale, x2
finale
|
2
|
|
|
|
- t1 tempo-istante iniziale, t2
finale
|
2
|
|
|
|
|
|
|
200
|
p4
|
- a = accelerazione del moto di un punto mobile
|
2
|
14
|
|
|
- Dv variazione di velocita' del moto
|
2
|
|
|
|
- Dt variazione di tempo del moto
|
2
|
|
|
|
- v1 velocita' iniziale, v2
finale
|
2
|
|
|
|
- t1 tempo-istante iniziale, t2
finale
|
2
|
|
|
|
|
|