^^Angolo alla circonferenza, mobile coi piedi fissi, fa il giro.

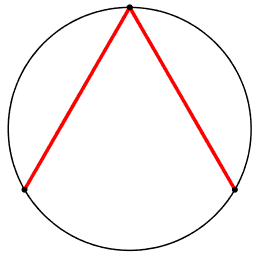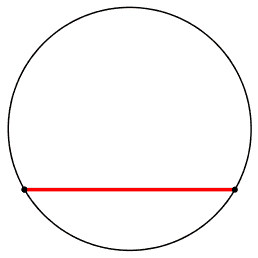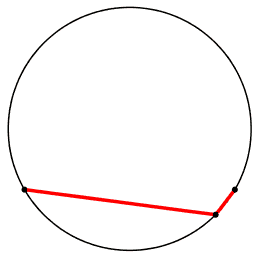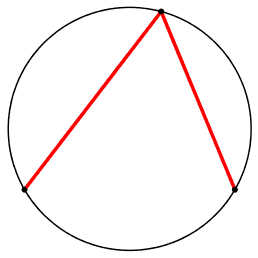
pensiamo brevemente a tutte le possibili figure assunte ...

Poi iniziamo ad osservare un caso

"nudo"	"arricchito"

dis: ang_crc.ggb usando come slider ixβV, e dis-attivando la visibilita' degli accessori.

Note sul disegno

aggiunti elementi non del testo, per arricchire l'ambiente, di solito favorisce la comprensione, se non fuorviante o eccessivo.

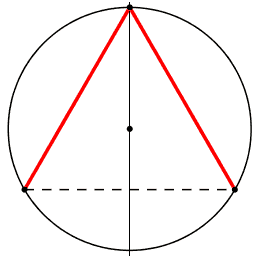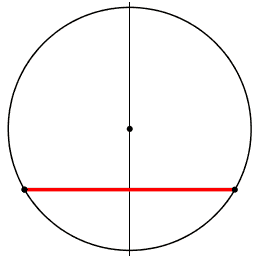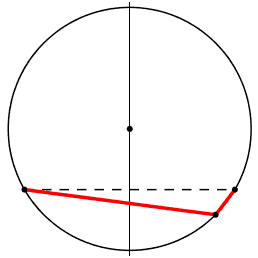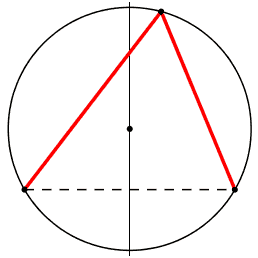
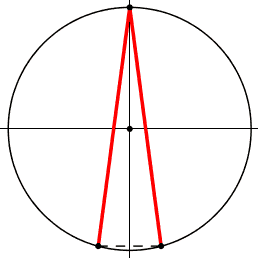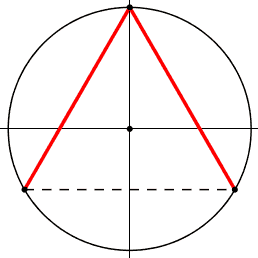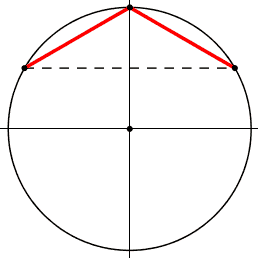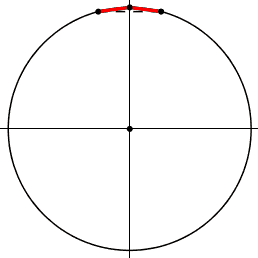
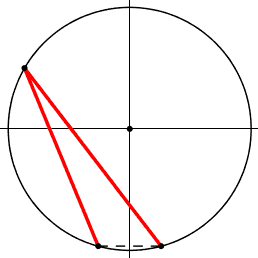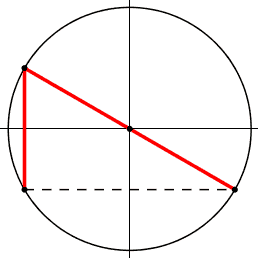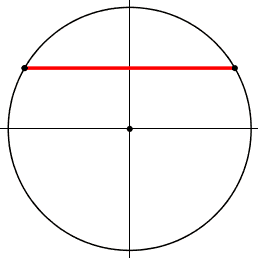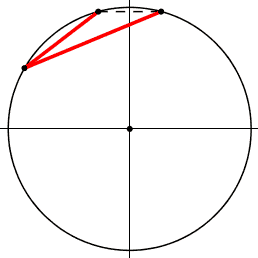
1) i piedi dell'angolo sono uniti da un segmento tratteggiato,
nm: corda, corda di base, o base, dell'angolo alla circonferenza.

2) centro della circonferenza

3) asse di simmetria; lo chiamo cosi' poiche' per ogni angolo in un lato esiste il simmetrico-riflesso nell'altro.

Il disegno (dinamico) rappresenta tutti i casi possibili?

precisamente: il caso qualsiasi si puo' riportare al caso presente?

1. il giro e' fatto da una infinita' di stati-configurazioni, quindi per rappresentare e' inevitabile campionare, qui 24 campioni.
2. con una opportuna rotazione, dal caso qualsiasi, si portano:
   • piedi su retta orizzontale, nel semicerchio inferiore

   pero' possono essere ad altezze diverse.

Notiamo che la famiglia di figure generate ha anche una simmetria-riflessione con l'asse parallelo alla corda e passante per il centro del cerchio.

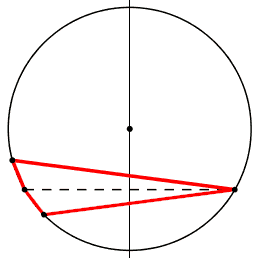
dis: ang_crc.ggb usando come slider ixβCorda

dida: abbiamo esplorato i vari casi, e organizzati, con un percorso esplorativo; non e' l'unico. E' quello che mi e' stato spontaneo, e parso il piu' conveniente.

Osservazioni (come vengono, poi si organizzano man mano)

1. l'angolo mobile sembra costante in ampiezza,
   quando si muove in una parte
   • della circonferenza, divisa dall'altra dai piedi dell'angolo.
   • equi: del cerchio, divisa dall'altra dalla corda di base.
2. l'angolo e' minore nella parte maggiore
   l'angolo e' maggiore nella parte minore
   l'angolo non esiste quando il vertice si sovrappone ad un piede.
3. Il cambiamento da un'ampiezza all'altra avviene con una discontinuita', cioe' il valore cambia "con un balzo" da una valore ad un altro senza assumere i valori intermedi.
   dida: e' un buon esempio per illustrare la discontinuita' di una funzione definita (parzialmente) sulla circonferenza.
   • come spiegare la discontinuita' di variazione?
   • quanto vale la variazione?
   • quale funzione uno dell'altro?
4. 2 angoli a vertice, con gli stessi piedi, uniti fanno un Quadrilateo ciclico
   • quadrilatero semplice se stanno in parti opposte della base
   • quadrilatero intrecciato se stanno dalla stessa parte della base

Osserviamo meglio l'angolo

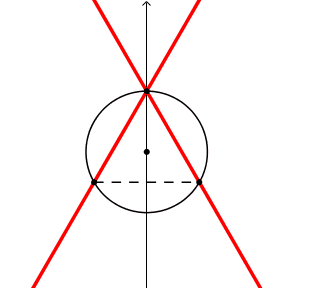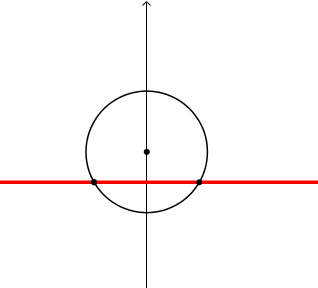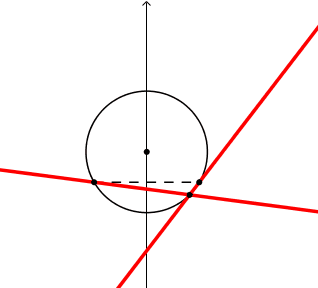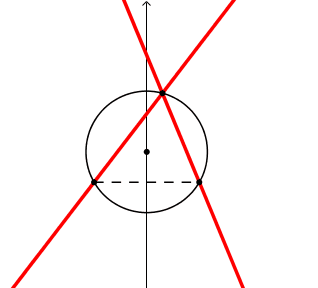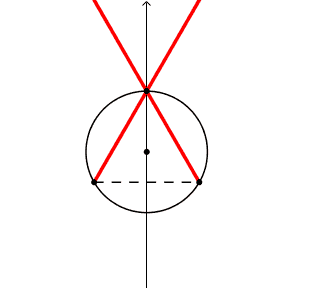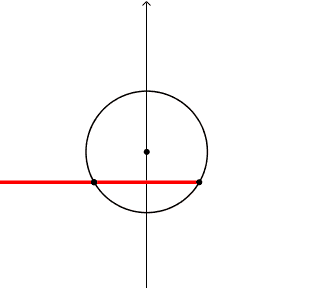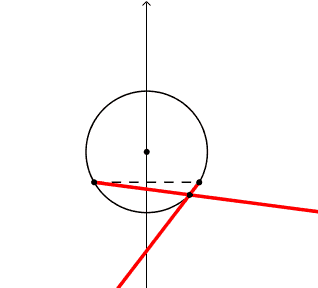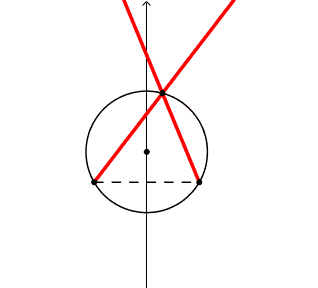
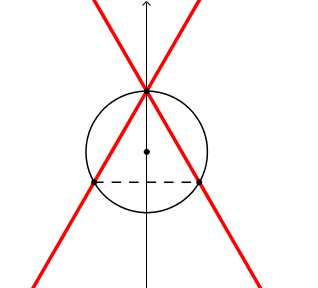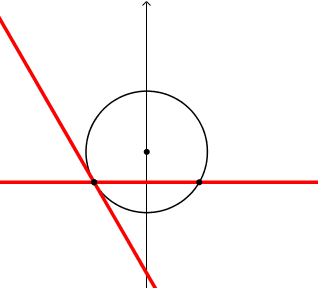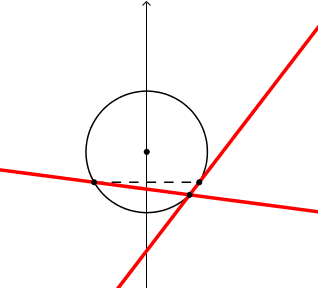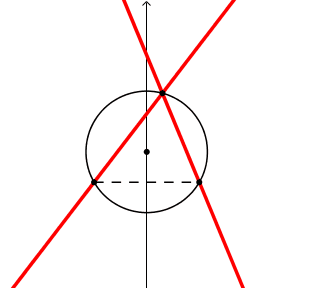
Prolunghiamo i lati dell'angolo a rette. La figura guardate nell'insieme "2 rette incrociate" sembra rigida, cioe' con gli angoli dell'incrocio costanti; sono gli angoli alla circonferenza. La retta-lato scompare quando il vertice si sovrappone al piede, e quindi non esiste il segmento-lato e quindi la sua retta prolungamento.

Si possono percepire aspetti diversi a seconda di dove si mantiene continuita' di osservazone. es:

• angolo alla circonferenza entro il cerchio, che cambia ampiezza
• un angolo dell'incrocio delle 2 rette, sempre quello.

Si puo' cosi' farsi un'idea della discontinuita' del valore dell'angolo alla circonferenza passando da una parte all'altra della corda di base.

Per capire meglio faccio delle variazioni di disegno

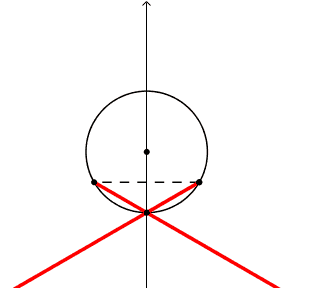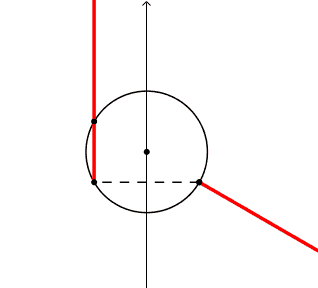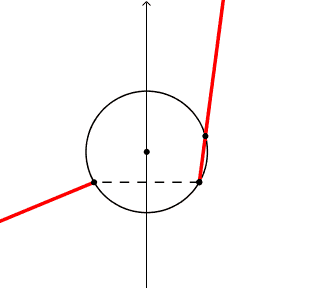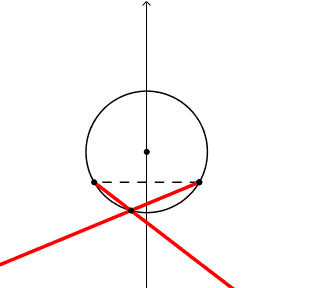
Prolunghiamo i lati dell'angolo a semirette uscenti dal piedi. La rigidita' degli angoli all'intersezione delle semirette e meno evidente che nel caso delle rette.

Rette ruotanti con uguale velocita' di rotazione

quindi l'angolo tra le rette rimane costante poiche' gli spostamenti angolari di entramne le rette sono uguali.

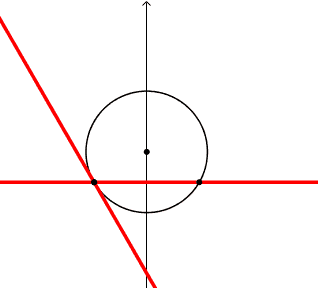
ang_crc_rette.ggb | ang_crc_rette_rot.ggb

nm usata nel documento GeoGebra

CordaA CordaB sono punti, iniziano in maiuscolo, estremi di cordaSeg
CX punto preso come riferimento angolare di centro C

Rotate(Line(CordaA, CX), βV / 2, CordaA)  accettata da GG
Rotate(Ray(CordaA, CX), βV / 2, CordaA) non piace a GG, la riscrive
Ray(Rotate(CordaA, βV / 2, CordaA), Rotate(CX, βV / 2, CordaA))
io l'ho riscritta

Ray(CordaA, Rotate(CX, βV / 2, CordaA)) 

fa ruotare raggio uscente da CordaA poiche segue la rotazione dell'img di CX
potrei riscrivere nello stesso stile anche la prima
Line(CordaA, Rotate(CX, βV / 2, CordaA))

Le semirette opposte
srettaA' = Ray(CordaA, Rotate(CX, (βV / 2) + pi , CordaA))
srettaB' = Ray(CordaB, Rotate(CX, (βV / 2) + pi , CordaB))

 

Relazione tra le 2 ampiezze dell'angolo alla circonferenza

angolo alla circonferenza in 2 stati:

in prossimita' del "salto della corda", prima e dopo,
coi vertici che tendono allo stesso piede

A occhio:

1. tende al triangolo poiche' i lati corti tendono ad allinersi
2. l'angolo dei lati lunghi tende a 0 (quindi per i rimanenti 2, la somma tende al piatto)
3. 1e2 implica:
   la somma dei 2 angoli al vertice tende a 1 angolo piatto.

una dimostrazione dettagliata e formale negli apporfond.

Dirlo

Dirlo

Angolo sulla circonferenza, piedi fissi, il vertice mobile fa il giro della circonferenza

Note sul disegno

esistono elementi aggiuntivi non del testo, ma arricchisce l'ambiente, e di solito favorisce la comprensione, a meno che non diventi distogliente.

Dirlo

1. Angolo mobile sulla circonferenza, con piedi fissi, fa il giro.
2. Angolo mobile sulla circonferenza fa il giro (con piedi fissi)

Dirlo

1. Il cambiamento da un'ampiezza all'altra avviene con una discontinuita'.
2. Cambiamento con discontinuita' da un'ampiezza all'altra.

Dirlo

1. Angolo mobile sulla circonferenza fa il giro (coi piedi fissi).
2. Vertice mobile di angolo alla circonferenza fa il giro (coi piedi fissi).
3. Vertice mobile di angolo alla circonferenza coi piedi fissi, fa il giro.
4. Angolo alla circonferenza, mobile coi piedi fissi, fa il giro.

Approfond

Relazione tra le 2 ampiezze dell'angolo alla circonferenza

1. il vertice tende ad un piede

   equi: il lato corto tende a lunghezza 0

   equi: l'angolo tra il lato lungo e la corda tende a 0
   equi: il lato lungo tende alla corda

2. i 2 lati corti, prima e dopo, tendono ad essere allineati

   equi: il loro angolo CC tende a 1 piatto
   il quadrilatero tende a trilatero

3. i 2 lati lunghi, prima e dopo, tendono a sovrapporsi

   equi: l'angolo LL tra loro tende a 0

    

I 2 angoli prima e dopo, uniti fanno un quadrilato

Teo: quadrilato,  somma angoli interni = 2 piatti.

CC + LL + Aprima + Adopo = 2 piatti

Teo: il limite della somma e' uguale alla somma dei limiti

Teo: il limite di una variabile costante e' il valore della costante.

Sostituisco alle variabili il valore dei limiti

1piatto + 0 + Aprima + Adopo = 2 piatti

Aprima + Adopo = 1 piatto    Q.E.D.

il lato corto tende alla retta tangente alla circonferenza nel piede

il lato corto e' quasi tangente alla circonferenza

Talk

Chi mi sta di fronte ?

sono in cerchio con 24 persone.

Io sono il numero 1, alla mia destra il numero 2, e la numerazione prosegue cosi' progressivamente: alla dx del nr 2, il nr 3, e cosi' via, tutti sono numerati.

Chi mi sta di fronte?

Dimostrazione coi limiti

Teo: quadrilato,  somma angoli interni = 2 piatti.

Corollario: se in un quadrilato un angolo interno tende a 1 piatto, la somma degli altri 3 tende a 1 piatto.

Teo: se la somma di 3 angoli tende a 1 piatto, e 1 tende a 0, la somma dei 2 rimanenti tende a 1 piatto.

Generalita' del disegno (dinamico)

Il disegno (dinamico) rappresenta tutti i casi possibili?

diamo per scontato che il giro, che in effetti e' fatto da una infinita' di stati-configurazioni, e' completamente rappresentato dai campioni presentati, 24.

Il caso qualsiasi si puo' riportare al caso presente?

con una opportuna rotazione:

piedi su retta orizzontale, nel semicerchio inferiore.

Osservazioni (come vengono, poi si organizzano man mano)

1. nella parte maggiore, l'angolo e' minore
   nella parte minore, l'angolo e' maggiore
   quando il vertice si sovrappone ad un piede, l'angolo non esiste.