^^y=kx   k= 2  1/2  3  1/3. .ods|pdf

>>> k con segno

 

Scala monometrico, 1cm:1   Scala y:  1cm:2 invece di 1cm:1
 
     
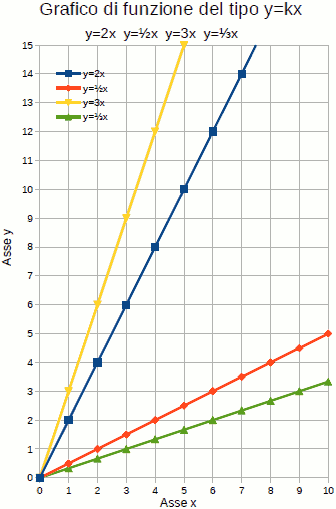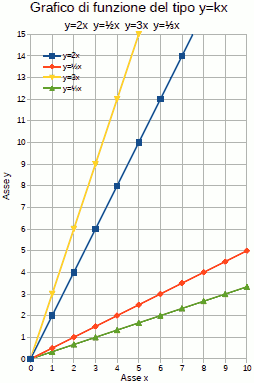
  • fondo scala 15
  • non ci stanno tutti i dati
  • grafico monometrico
  
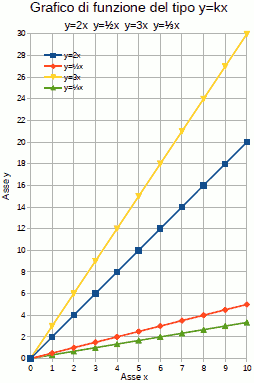
  • fondo scala 30
  • ci stanno tutti i dati
  • grafico non monometrico
  • uguale rapporto di scala x: 1cm:1
  • uguali dimensioni in cm: Lx=10, Ly=15
  • diversa scala y, nel rapporto di scala, e fondo scala
x y=2x y=½x y=3x y=⅓x
0 0 0 0 0
1 2 0,5 3 0,3
2 4 1 6 0,7
3 6 1,5 9 1
4 8 2 12 1,3
5 10 2,5 15 1,7
6 12 3 18 2
7 14 3,5 21 2,3
8 16 4 24 2,7
9 18 4,5 27 3
10 20 5 30 3,3

c1:  tb, x= 0 1 2 3 ... 10  y=2x; grafico. Ripetere con y=(1/2)  y=3x  y=(1/3)x .

Scala x: 1cm:1, Lx=10; scala y: 1cm:2, Ly=15, per farci stare anche il dato y massimo, che e' y=3*10=30.

c2: ripetere c1, ma tutto uguale, solo rapporto di scala x: 1cm:1.

Per fare un grafico monometrico 1cm:1, di dimensioni uguali al precedente, Lx=10, Ly=15, per confrontarli.

Eseguiti in 2 lezioni consecutive

Questi 2 compiti sono assegnati contemporaneamente, perche' favorisce la loro comprensione, ma e' richiesto di eseguirli in 2 lezioni consecutive.

Conclu

anche cambiando rapporto di scala, i grafici rettilinei rimangono rettilinei !

sebbene diversamente inclinati.

VrfCrz

  1. C'e' chi continua a tracciare i punti singoli, invece che la retta.
    Es: Lucetti
  2. Anche se prendo un punto interno, la retta va continuata fino al bordo

 

Come calcolare il punto di intersezione con il bordo superiore ?

Es: Dalle Mura ha evitato il problema scegliendo un punto prossimo ad occhio. con x intero.

Crz

  1. Posizione grafico: la peggiore e' in basso-sx, non c'e' spazio per i numeri di scala e coordinate.
  2. Approssimare alla fine sul conto esatto, non: calcolare sui numeri approssimati all'inizio.

    Studiamo come approssimare la funzione y=⅓x.

  3. bene: uso colori; coordinate su piu' livelli.

 

L'interessante errore di Poli

 

Link

 | Confrontare tra loro le figure dilatate 1D oriz, 1D vert, 2D, sullo sfondo del reticolo quadro ugualmente dilatato.

 

 

Guida ins

Info aggiuntive

Se lo studente sa gia' che y=kx ha grafico rettilineo, si puo' disegnare la retta senza disegnare tutti i punti del grafico.

Scopo di questo ecz

Lo scopo varia a seconda del grado di conoscenze dell'allievo.

  1. Disegnare un grafico cartesiano di funzione
  2. y=kx ha come grafico cartesiano una retta passante per l'origine
  3. anche cambiando rapporto di scala, i grafici rettilinei rimangono rettilinei !
    c: questo e' lo scopo originale per cui e' stato creato l'ecz

In una programmazione accurata,

potrebbe essere spezzato in 2: aver gia' fatto quello monometrico, con lo scopo di studiare la funzione y=kx, e poi porsi la questione di "come appaiono i grafici modificando le scale".

Ma io ho avuto questa 2a iti senza averla avuta l'anno precedente.

Nella mia programmazione ideale (in progress) l'inizio dell'argomento e':

Proporzionalita': incrementi costanti a partire da zero.

 

Titolo

  1. y=2x  y=(1/2)x  y=3x  y=(1/3)x
    c: titolo originale, sottolineava con la ripetizione della scrittura di funzione, che erano funzioni diversi
  2. y=kx  k= 2  1/2  3  1/3
    c: questa scrittura privilegia invece la familiarita', ma il motivo per cui l'ho scelta e' che e' piu' contratta, e mi sembra piu' leggibile complessivamente.

 

Talk

Dis

zoom 66,7%