| f = | T R |
= | Tδ Rδ |
= | F L |
 |
|
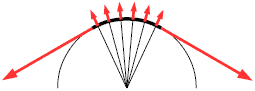
La forza fatta da un arco e' un caso particolare di Forza fatta dall'angolo di una fune con tensione ai capi uguale.
| 1 | F = 2Tsen(δ/2) | Forza fatta dall'angolo una fune con tensione uniforme |
| 2 | Riconosciamo la geometria del
Settore circolare angolo di deviazione della fune e' = all'angolo al centro dell'arco |
|
| 3 | Minore e' l'angolo dell'arco, minore e' la densita' di forza | |
| 4 | F = Tδ | approssimazione piccoli angoli senβ≈β |
| 5 | L = Rδ | lunghezza dell'arco |
| 6 | f = T/R | densita' di forza, rapporto membro a memrbro 4 e 5 |
La densita' di forza perpendicolare alla forza di tensione della fune, ne varia la direzione esattamente nella nuova direzione della fune, ma non ne cambia l'intensita', proprio perche' agisce perpendicolarmente.
Nel caso di una linea a curvatura variabile, basta considerare la circonferenza osculatrice.
Quello presentato nella parte principale e' piu' guidato dalla curiosita' del risultato semplice e veloce
| 1 | idem | |
| 2 | ||
| 3 | ||
| 4 | L= δR | lunghezza dell'arco |
| 5 | f= F/L = T/R 2Tsen(δ/2)/(δR) |
densita' di forza |
| 6 | sen(δ/2) ≈ δ/2 | approssimazione piccoli angoli senβ≈β |
| 7 | f= T/R | approssimazione piccoli angoli |
| f = | F L |
= | T R |
| f = | T R |