| P | 1 | 2 | 3 | ... |
|---|---|---|---|---|
| x | x1 | x2 | x3 | |
| y | y1 | y2 | y3 |
inseriamo il poligono in un piano cartesiano; siano date le coordinate della successione di punti-vertice della poligonale perimetro del poligono; cio' si puo' fare con strutture dati diverse, qui per fissare le idee una tb.
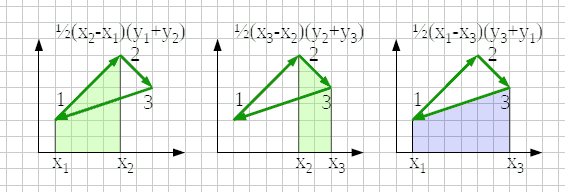
area "sotto" un lato arriva fino all'asse x orizzontale, e forma un trapezio;
Area trapezio = ½(B1+B2)H, qui H e' orizzontale, B verticale

l'area sottesa a un lato e' intesa col segno!
½(xi+1 - xi)*(yi
+ yi+1)
il perimetro deve essere percorso in senso orario
lato discorde al verso x ~ area negativa
lato concorde al verso x ~ area positiva
tradotto in coordinate:
∆x incremento x del vertice, negativo ~ area negativa
| 1 2 |
n | ||||
| A = | ∑ | i | (xi+1 - xi)*(yi + yi+1) n+1 ≡ 1 | ||
| 1 |
(x1,y1) (x2,y2) ... (xn,yn) |
elenco dei vertici muovendosi lungo il perimetro, partendo da un vertice a piacere. |
l'area del poligono e' uguale alla somma algebrica dell'area dei trapezi, ognuno sottostante un lato del poligono.
E' l'idea di calcolo condivisa da Area del poligono e Area sottesa ad un poligonale.
| = | + |
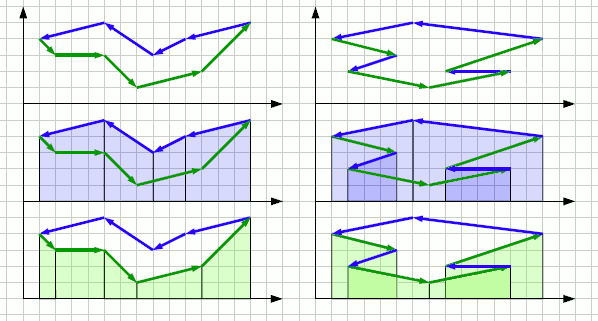
poligonale sovrastante
poligonale sottostante |
| = | - |
area sottesa alla poligonale soprastante
area sottesa alla poligonale sottostante |
il poligono a sx e' concavo; il poligono a dx ha punti di inversione del moto sul bordo poligonale oltre quelli dell'estremo sx e dx, che producono ulteriori sovrapposizioni dei trapezi.
Bivettore, area; nel piano cartesiano; metodo dei trapezi.
Area di un poligono, shoelace formula.

| 1 2 |
n | ||||
| A = | ∑ | i | (xi+1 - xi)*(yi + yi+1) n+1 ≡ 1 | ||
| 1 |
| 1 2 |
n | ||||
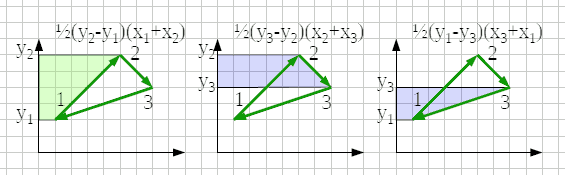
| A = - | ∑ | i | (yi+1 - yi)*(xi + xi+1) n+1 ≡ 1 | ||
| 1 |
Non e' detto che sia una funzione y=f(x) poiche' ad uno stesso valore di x possono essere associati 2 diversi punti e quindi 2 valori diversi di y.
| poligonale = | + |
poligonale sovrastante
poligonale sottostante. |
e' un modo di guardare-pensare al poligono che e' conveniente.
| poligonale = | + |
poligonale sovrastante
poligonale sottostante |
vale a condizione di poligonali non intrecciate.
area del poligono
| (x1,y1) (x2,y2) ... (xn,yn) | elenco dei vertici muovendosi lungo il perimetro, partendo da un vertice a piacere |