^^Area sottesa ad un polisegmento.

Idea: Area sottesa divisa in trapezi

  

(x1,y1)  (x2,y2)  ...  (xn,yn)  

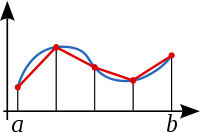
coordinate dei punti della poligonale
in ordine di x crescente

sommando l'area dei singoli trapezi:

  1
2		 n-1      
A =   ∑ i   (xi+1 - xi)*(yi + yi+1)
  1      

 

sviluppando e semplificando, si ottiene

A= - 1

2

 | x1 x2 ... xn | +xnyn -x1y1
y1 y2 ... yn

But what does that mean?

The notation is meant to be suggestive of a determinant.

It’s not literally a determinant because the matrix isn’t square. But you evaluate it in a way analogous to 2 by 2 determinants: add the terms going down and to the right, and subtract the terms going up and to the right

Dimostrazione semplificazione formula

(x2-x1)(y1+y2)  +x2y1 +x2y2 -x1y1 -x1y2

(x3-x2)(y2+y3)  +x3y2 +x3y3 -x2y2 -x2y3

(x4-x3)(y3+y4)  +x4y3 +x4y4 -x3y3 -x3y4

(x5-x4)(y4+y5)  +x5y4 +x5y5 -x4y4 -x4y5

(x6-x5)(y5+y6)  +x6y5 +x6y6 -x5y5 -x5y6

 

(x1-x6)(y6+y1)  +x1y6 +x1y1 -x6y6 -x6y1  caso poligonale chiusa

 

Links

  1. Area del trapezio e del politrapezio.
  2. Area di un poligono, metodo delle coordinate.

 

Approfond

 

Area sottesa divisa in trapezi, cioe' vederci un "politrapezio".

"Politrapezio" e' un mio neologismo.