| C&N: | ___-___-07 Clas_4__LST |
| Corregge: | p: e: voto: |
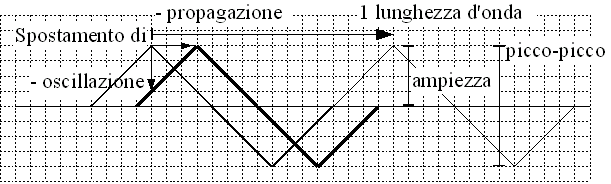
| 876 Definizione di: struttura e moti dell'onda, tramite disegno. | 8 | |

|
4 | |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | ||
| 50 | Il tappo di sughero che galleggia sul mare, quando arriva l'onda | 8 | |
| non viene portato via dall'onda che passa | 2 | ||
| invece quello sul fiume viene portato via dalla corrente | 2 | ||
| Si muove su e giu', e un po' avanti e indietro | 1 | ||
| circa un'ellisse piu' alta che larga. | 1 | ||
| Il tappo indica il moto del materiale dell'onda | 1 | ||
| poiche' si muove attaccato ad esso | 1 | ||
| 60 | L'onda del mare si puo' simulare con una "ola" di persone | 1 | |
| 70 | Il termine "onda" riferisce: sia la singola onda, | 1 | 2 |
| che tutto il treno d'onde | 1 | ||
| 80 | Osservare l'onda generata dal sasso nello stagno: | 8 | |
| 1: si puo' simulare con un cerchio di persone | 1 | ||
| 2: in ogni punto del fronte d'onda, la direzione di propagazione | 2 | ||
| e' perpendicolare al fronte | 1 | ||
| 3: l'ampiezza dell'onda diminuisce al progredire del fenomeno | 2 | ||
| 4: la velocita' di propagazione rimane costante, anche se 3 | 2 | ||
| 90 | Le onde del mare che si avvicinano alla spiaggia, se sono piccole si nota che: | 7 | |
|
- diminuiscono di velocita' |
2 | ||
| - e: cambiano direzione: | 1 | ||
| il fronte d'onda tende a diventare parallelo alla riva, | 2 | ||
| la direzione di propagazione perpendicolare alla riva | 2 | ||
| 310 |
Il punto di taglio delle lame della forbice quando taglia, si muove |
4 | |
| cosi' come il punto di contatto della ruota che gira sulla strada, | 1 | ||
| cosi' come la cresta dell'onda nel moto di propagazione | 2 | ||
| ma non sono punti materiali , bensi' punti geometrici | 1 | ||
| 340 | Le onde hanno associati 2 movimenti: | 8 | |
| 1: moto di propagazione, globale, di uno stato fisico | 3 | ||
| 2: moto di oscillazione, locale, del materiale | 3 | ||
| 1 Meglio detto: moto di propagazione del PROFILO dell'onda, | 1 | ||
| poiche' sottolinea che e' il profilo a muoversi e non la materia. | 1 | ||
| 360 | Un'onda e' (by RO) lo spostarsi di luogo di uno stato del luogo | 2 | 4 |
| questo e' il moto di propagazione. | 1 | ||
| es: un'onda di temperatura quando riscaldo il fondo di una padella. | 1 | ||
| 370 | La onde trasportano energia , non materia | 2 | |
| 380 | La velocita' di propagazione del suono in aria, in condizioni normali, e' di: 340 m/s | 1 | |
| 400 | Consideriamo un'onda periodica. La velocita' si puo' ricavare con la formula: | 4 | |
|
- v= s/t = λ/T (λ lambda = elle greca, minuscola, chi vuole scriva L) |
2 | ||
| dove: - λ lunghezza d'onda | 1 | ||
|
- T periodo dell'onda |
1 | ||
| 410 | Onda ciclica si propaga di N= 5 onde in t= 4s, con una spostamento complessivo LN= 2m. | 13 | |
| 1: periodo: T= t/N = 4s/5 = 0,8 s | 2 | ||
| 2: def: frequenza: f= N/t = 5/4s = 1,25 Hz | 2 | ||
| frml: frequenza: f = 1/T = 1/0,8s = 1,25 Hz | 2 | ||
|
3: lunghezza d'onda: λ= LN/N = 2m/5 = 0,4 m |
2 | ||
| 4: def: velocita': s/t = 2m/4s = 0,5m/s | 2 | ||
| frml: velocita': s/t = (N*λ)/(N*T) = λ/T = 0,4m/0,8s = 0,5m/s | 3 | ||
| 200 | Scegli il tipo di onda. T=trasvers L=longitud D=dipende | 2 | |
| onde marine T onde su una molla D | |||
| onde sonore in aria L onde elettromagnetiche T | |||
| 202 | Onda longitudinale e onda trasversale. La classificaz si basa su: direzione dei 2 moti, | 1 | 6 |
| di propagazione e di oscillazione, uno rispetto all'altro | 3 | ||
| - onda trasversale: trasversali | 1 | ||
| - onda longitudinale: longitudinali | 1 |
Extra:
| 300 | Consideriamo un'onda periodica, 2 punti dell'onda: | 4 | |
|
- "punti in fase": spostamenti oscillatori uguali (sempre) |
1 | ||
| - "punti in opposizione di fase": spostamenti oscillatori opposti (sempre) | 1 | ||
| Condizione perche' 2 punti siano in fase: distano 1 lunghezza d'onda, | 1 | ||
|
o un suo multiplo |
1 | ||
| 310 | Condizione perche' 2 punti di un'onda sinusoidale siano in opposizione di fase: | 2 | |
| distano 1/2 lunghezza d'onda | 1 | ||
| piu' un multiplo di lunghezze d'onda. | 1 | ||
| 405 | La velocita' dell'onda: | 3 | |
| - e' costante nei mezzi omogenei | 1 | ||
| - e' indipendente dall'ampiezza nei mezzi lineari | 1 | ||
| - nella corda aumenta all'aumentare della tensione | 1 | ||
| 345 | Nel caso di onde cicliche, cosa fanno i moti: | 2 | |
| - in 1 ciclo il moto di propagaz avanza di 1 lunghezza d'onda | 1 | ||
| - e contemporaneamente il moto oscillatorio compie 1 ciclo | 1 |
Extra libero:
| Griglia di valutazione del disegno | 8 | ||
| 1 | 4 punti per le 6 parole, 1 punto in meno per ogni mancanza, fino a 0 | 4 | |
| 2 | spostamento di 1 lunghezza d'onda segnato corretto | 1 | |
| 3 | spostamento di propagazione segnato corretto | 1 | |
| 4 | spostamento di oscillazione segnato corretto | 1 | |
| 5 | ampiezze esatte | 1 |
Un'onda piana in un ondoscopio passa da una zona d'acqua piu' profonda, ad una meno profonda, con un angolo di incidenza di 45�, e la sua velocita' dimezza. f1 = frequenza onda incidente, f2 = rifratta
| f1/f2 = | (a) =1 | (b) =1/2 | (c) = 2 | (d) = (√2)/2 | (e) = 2/(√2) |
Un'onda piana di lunghezza d'onda λ, incontra fenditura parallela ai fronti d'onda e larga L. La diffrazione:
(a) e' trascurabile se λ e' grande, qualsiasi sia la L
(b) dipende dal rapporto λ/L
(c) e' rilevante qualunque sia λ, purche' L sia piccolo
(d) aumenta solo al diminuire di λ, qualunque sia la larghezza della fenditura
2 sorgenti puntiformi SA SB di uguale ampiezza e fase, e λ=3,0 cm, e separazione d=1,5 cm. Un punto P, situato sulla prima frangia costruttiva dopo quella centrale, dista 15 cm da SA. Quanto dista da SB?
Interferenza di 2 fenditure. Distanza tra le fenditure: d=0,1 mm. Seguendo l'asse geometrico delle 2 fenditure, per 5 m, e deviando ortogonalmente di 20 cm, si giunge al punto P in cui si ha il primo massimo di interferenza, a lato di quello centrale. Calcolare λ.
Extra
Due impulsi sinusoidali si propagano lungo una fune in verso opposto. Dopo essersi sovrapposti:
(a) continuano a propagarsi con le stesse caratteristiche
(b) se sono uguali si annullano a vicenda e la fune rimane immobile
(c) continua a propagarsi solo quello di ampiezza maggiore e l'altro viene annullato
(d) la velocita' di propagazione dimuisce
Che formula e'?
| √(T/μ) | |
| √(k/ρ) | |
| √(k/m) | |
| ∆p/(∆V/V) | |
| sen(ωt) | |
| sen(kx) | |
| n(λ/2)=L |
c: mi sembra un po' sbilanciata a favore delle semplici parole