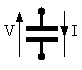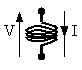C&N: ___-___-07  Clas_5__LST
Corregge: p:           e:          voto:
Titolo: Elettromagnetismo, regime variabile.
796 Si parla di regime costante o regime variabile secondo che le grandezze elettriche v e i 2 11
 siano costanti o variabili rispetto al tempo  
  Formule base per il comportamento elettrico in regime variabile, nel campo d'uso    
elettrotecnico e elettronico 1
resistore ohmico:  v=R*i                v(t)=R*i(t)   3
condensatore:  q=C*v          q(t)=C*v(t) 3
induttore: φ=L*i             φ(t)=L*i(t) 3
Notazione: variabili in minuscolo, costanti in maiuscolo 1
In sintesi: le stesse formule sono valide sia in regime costante che variabile 1
   
786 Formule differenziali per condensatore e induttore in regime variabile   12
   dv 
i=C*
dt
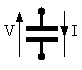poiche'  q=C*v

 

dq=C*dv 

dq dv
=C*
dt dt
5
   di 
v=L*
dt
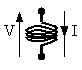poiche'  φ=L*i

 

dφ =L*di

dφ     di 
=L*
dt dt
5
  A differenza del regime statico dove: condensatore: I=0     induttore:  V=0 2  
768 Formula funzione sinusoidale del tempo, dello spazio, e funzione d'onda sinusoidale.   8
  Tempo: y(t)= YM*sen(ω*t+φ)     ω=2p/T 3  
  Spazio: y(x)= YM*sen(k*x+φ)     k=2p/λ 2  
  Onda=tempo+spazio:  y(x;t)= YM*sen(k*x-ω*t+φ) 3  
770 Traslaz grafico funzione: formula, interpretazione   9
  Temporale: ftrasl(t)= f(t-T)    T e' la traslazione, numero relativo  4  
  Interpretaz: T positivo, traslaz destra, ritardo 1  
  T negativo, traslaz sinistra, anticipo 1  
  Traslaz spaziale x: ftrasl(x)= f(x-λ)    λ e' la traslazione, numero relativo 1  
  Nel caso delle funzioni sinusoidali:  cos(x)=sen(x+p/2)=sen(x-(-p/2)) 1  
  cos e' in anticipo di p/2  rispetto a sen 1  
788 Alternatore, modello elementare. Situazione: 1: B uniforme     1 17
  2: asse di rotazione della spira perpendicolare a B 1  
  3: moto rotatorio uniforme 1  
  Flusso magnetico spira:  φ=B*A*cos(β)     β angolo tra B e il vettore area 4  
  In funz t: φ(t)= ΦM*cos(ω*t+β0)     ω=2p/T    ΦM=B*A 4  
  Tensione indotta: v= - dφ/dt= - ΦM*(-sen(ω*t+β0)*ω) 4  
  Notiamo: 1: la tensione indotta e' sinusoidale 1  
  2: e' proporzionale alla velocita' angolare di rotazione 1  
777 Definizione di intensita' di corrente elettrica, media e istantanea. Relazione integrale.   13
 
  ∆q
im = 
  ∆t
  dq     ∆q
ii = 
= limite 
  dt   ∆t→0   ∆t
  1   ∫ t1  
im =
*   i(t)*dt
  t1-t0   t0  
2
2

3

  
  Formula potenza elettrica assorbita da un bipolo, media e istantanea. Relazione integrale.    
 
  ∆E
pm = 
  ∆t
  dE     ∆E
ii = 
= limite 
  dt   ∆t→0   ∆t
  1   ∫ t1  
pm =
*   p(t)*dt
  t1-t0   t0  
1
1
3		  

 

 

127 Calcolo la corrente media di una corrente istantanea sinusoidale raddrizzata.   5
  1   ∫ p  
im =
*   A*sen(t)*dt
  p   0  
  1   |
|
|		 p
im =
*A*(-cos(t))  
  p   0
  2  
im =
*A
  p  
2
2
1		  
  Calcolo la potenza media di una corrente istantanea sinusoidale.   11
130
  1   ∫ p  
pm =
*   R*(I*sen(t))2*dt
  p   0  
  1   ∫ p  
=
*R*   I2*sen2(t)*dt
  p   0  
  2
2
  1   ∫ p  1-cos(2*t)   
=
*R*I2*  
*dt
  p   0 2  
  1   ( ∫ p   ∫ p     )
=
*R*I2*   dt  -   cos(2*t) *dt
  2p   0   0    
  2
2
  1  
=
*R*I2*(p-0)
  2p  
  1  
=
*R*I2
  2  
  2
1
124 La corrente efficace e' una corrente costante la cui potenza costante e' uguale   4
  alla potenza media della corrente variabile   5
 
  1  
R*Ie2 =
*R*I2
  2  
da cui
  IM  
Ie =
 
  √2  
3
2		  
137 Calcolare tensione e corrente per condensatore e induttore in regime sinusoidale.   11
 
   dv 
i=C*
dt
 v(t)= VM*sen(ω*t+φ)
 dv   
= VM*cos(ω*t+φ)*ω     
dt
4  
 
   di 
v=L*
dt
 i(t)= IM*sen(ω*t+φ)
 di   
= IM*cos(ω*t+φ)*ω     
dt
4  
  notiamo che: 1: tensione e corrente sono entrambi sinusoidali 1  
  2: sono sfasate di p/2  1  
  3: la relazione dipende da ω in modo direttamente o inversamente proporzionale 1  

 

746 Un solenoide di lunghezza 20 cm e' composto da 100 spire di area 10 cm2 ciascuna. Calcolare 1: induttanza; 2: flusso magnetico autoconcatenato quando I= 2A. Come si modificano tali valori se il solenoide e' avvolto su un nucleo di permeabilita' magnetica relatativa  μr=104?  
747 Calcolare la formula per l'induttanza di un solenoide.  
750 Moto di una carica in un campo magnetico.  
755 Moto di una carica in un campo elettrico.  
760 Effetto Hall.  
755 Calc campo magnetico generato da filo di corrente rettilineo infinito.  
760 Calc flusso campo elettrico carica puntiforme.