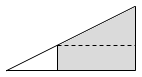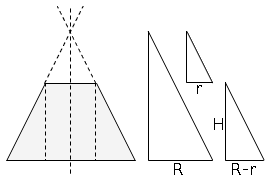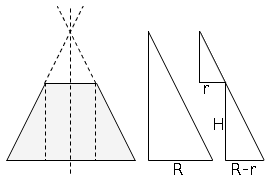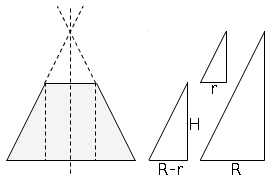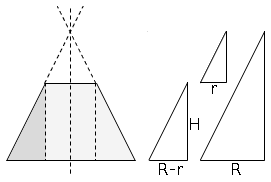
dida: disegnare i 3 triangoli separati facilita vedere le corrispondenze, ostacolate dal sovrapporsi dei tri.
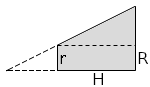
dida: le lettere facilitano.
L'idea brillante per calcolare l'altezza del cono generatore e':
 |
vedere 3 triangoli simili.
dida: disegnare i 3 triangoli separati facilita vedere le corrispondenze, ostacolate dal sovrapporsi dei tri.
dida: le lettere facilitano.
|
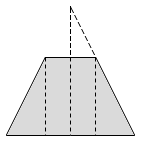
dida: Ambientare nell'usuale: permette alla percezione di richiamare in automatico tutti i meccanismi sviluppati in tale ambiente.
|
|
cono disposto "come il cerchio
trigonometrico",
per valutare l'angolo della retta generatrice rispetto all'asse. |
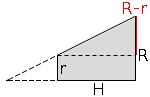 |
La pendenza del tronco di cono
>>>
|
Il coefficiente angolare della retta generatrice e'
| k = | R - r H |
= | R HG |
= | r Hp |
nm >>> |
Da cui si ricava:
| HG = | H R - r |
R HP = | H R - r |
r |
dim: linea logica.
⇒
basi invariate
altezze invariate
⇒
calcolo l'altezza del tri generatore, che e' anche quella del tri originale.
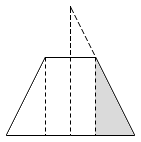
Propedeutico a questo, per imparare a vedere il trangolo "corolla, gonna"
p: calc lunghezza lato laterale.