 |
Esiste per ogni quadrilatero:
convesso, concavo, incrociato, non_piano.
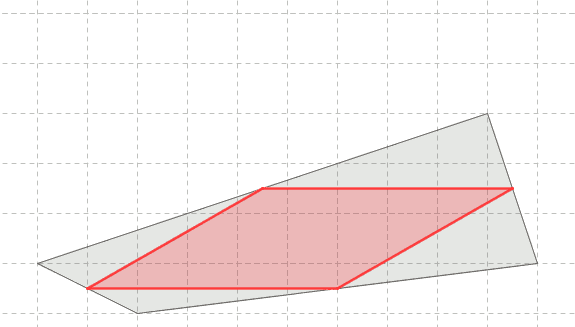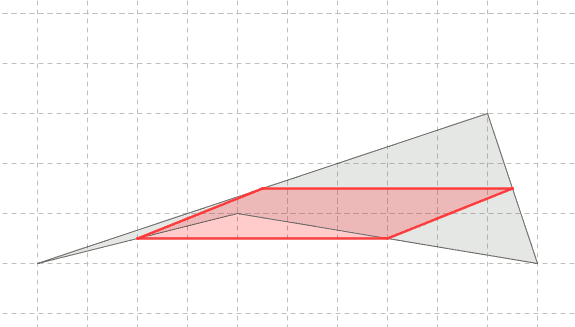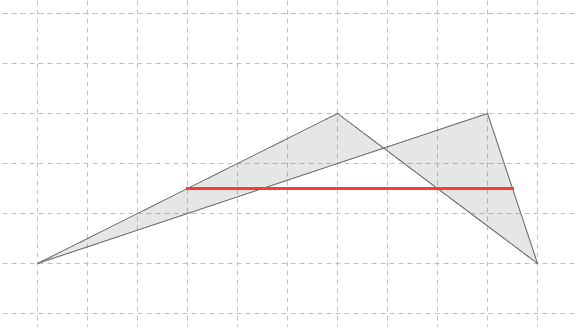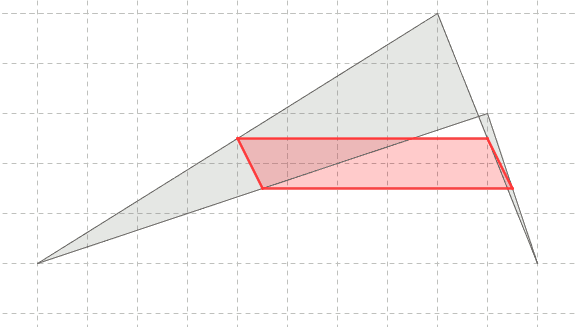
Per costruzione e' un quadrilatero, ed accade che sia un parallelogramma.
il parallelogramma dei punti medi l'ho scoperto circa nel 2015, eslorando con GeoGebra, e mi aveva abbastanza sorpreso, perche' non ne avevo mai sentito parlare, anche se mi rendevo conto che lo studio scolastico dei quadrilateri era molto parziale. Poi nell'estate del 2019, leggiucchiando su Wikipedia, d'estate un po' di tempo c'e', ed ora in vista della pensione ancora di piu', ho scoperto wp/Varignon's_theorem, ed ho visto che a parte il nome storico, la terminologia e' quella che avevo inventato.
L'incontro col parallelogramma non era casuale, ma il termine di un piccolo percorso
Fatto scoperto a seguito di Parallelogramma delle parallele alle diagonali di un quadrilatero.