^^Quadrati equivariano d'area ⇔  R(da,db) ?

Motivazione di questo studio  >>>

La famiglia di forme dei triangoli rettangolo, elencati con continuita'

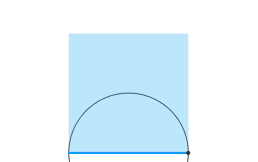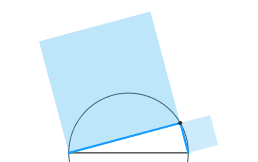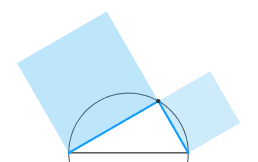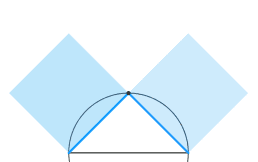
Triangolo rettangolo,
inscritto in una circonferenza,
il vertice retto mobile la percorre.

Ho fermato l'animazione li' perche' il resto lo posso immaginare-dedurre per simmetria.
Sono TUTTE le forme simili possibili di triangolo rettangolo, generate dal moto di deformazione continua-differenziabile della configurazione.

nm:  a b c, x y z  lunghezza di: cateto cateto ipotenusa;

da db dc, dx dy dz  differenziali di  a b c, x y z.

ẋ  ẏ   notazione di Newton per la derivata temporale di x(t) y(t)

a→0   a tende a 0 (zero)

I quadrati equivariano d'area  ⇔  R(da,db) ?

		Situazione qA quadrato piccolo cresce, qB quadrato grande decresce.   Variazione d'area in scuro bordi alto e destro.
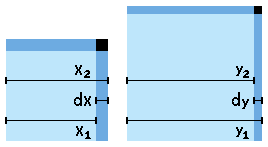		pedice1 := valore iniziale pedice2 := valore finale d  :=  variazione no segno   qA in  : 2x₁dx + (dx)² qB out: 2y₁dy - (dy)²
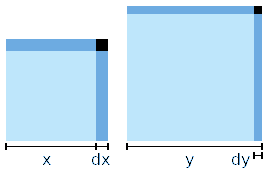		pedice no, e' l'usanza     qA in  : 2xdx + (dx)² qB out: 2ydy - (dy)²

qAin = qBout  equivariazioni d'area   

2xdx + (dx)²  =  2ydy - (dy)²

Ultimate equality: (discussa nell'approfond)
2xdx = 2ydy   equi  xdx = ydy.

Variazione del lato dei q, inv prop alla sua lunghezza.

Dopo averlo capito sembra intuitivo.

Varia di più il lato piu' corto, poiche' l'area che arriva dal lato piu' lungo si deve distribuire su una lunghezza minore.

Conclu

I quadrati equivariano d'area  ⇔  R(da,db):  a*da = b*db

la variazione di lunghezza dei cateti

provoca nei loro quadrati
variazioni di area opposte

Dida

Dirlo

1. i quadrati hanno uguali variazioni d'area
2. i quadrati variano d'area in ugual misura
3. i quadrati equivariano d'area
4. i quadrati si trasferiscono area
5. i quadrati variano d'area trasferendosela

Dirlo

1. impone una relazione tra da db
2. vincola tra loro da db

Dirlo

1. il moto del vertice rimanendo retto
2. il moto del vertice lo conserva retto
3. il vertice si muove rimanendo retto

Dirlo

1. Triangolo rettangolo
   inscritto in una semicirconferenza,
   con vertice retto mobile che la percorre
2. Triangolo rettangolo, il vertice retto percorre una circonferenza.

    

3. Triangolo rettangolo inscritto in una circonferenza, il vertice retto la percorre.

Dirlo

1. La famiglia di forme dei triangoli rettangolo, elencati con continuita'.
2. La famiglia di forme dei triangoli rettangolo elencati, con continuita'.
3. La famiglia di forme dei triangoli rettangolo, elencata con continuita'.

Talk

Dis

pit_teo_newton_x1dx_y1d.xcf

Proporzionalita'

xA:xB = yA:yB = m      xA*yB=xB*yA

xA:yA = xB:yB = k   

variazioni d'area dei quadrati correlano con
variazioni di lunghezza dei lati

Variazioni d'area uguaii, opposte in verso, una in diminuire, l'altra in aumentare.

Le variazioni di lunghezza dei cateti devono essere tali da produrre variazioni d'area dei loro quadrati, opposte.

96:2 = 48     x3 = 144

96:3 = 32    

90:2 = 45     x3 = 135       90*12

90:3 = 32                          (90*3/2)*(12*2/3)

Figura migliorabile

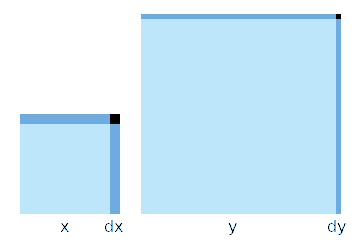
variazione di area di un quadrato
(x+dx)² = x² +2xdx + (dx)²

espo migliorabile.
I quadrati equivariano d'area  ⇔  R(da,db):  a*da = b*db

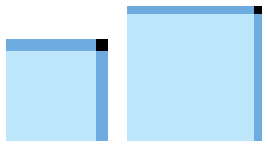qA quadrato piccolo cresce,
qB quadrato grande decresce.

Bordi alto e destro scuri;

turchese scuro + quadratino nero,
è l'area trasferita a qA da qB.