^^Pythagorean theorem, Newton style. Pre.

L'inizio di questa ricerca e' stato

il desiderio di inventare una dimostrazione del teo(rema) di Pitagora basata sulle VARIAZIONI-TRASFORMAZIONI piuttosto che sugli STATI.

Questo e' un atteggiamento generale sviluppatosi nel confronto della geometria euclidea, per accostarle la visione differenziale.

In accordo con un altro principio del formare al conoscere

• meglio dimostrare in modi diversi lo stesso teorema,

     che con lo stesso metodo dimostrare piu' teoremi
     (cio' risponde piu' all'utile).

Nell'educazione scientifica, conoscenza ed utilita' vanno consapevolmente commisurati.

La prospettiva scolastica specifica che ho ricevuto

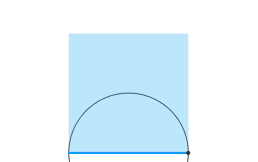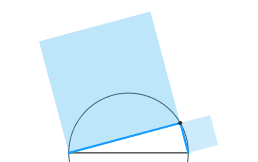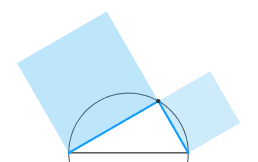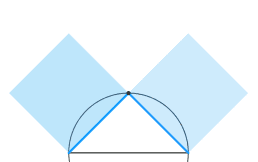
Teo Pitagora: in un triangolo rettangolo

• la somma dei quadrati dei cateteti
      e' uguale al quadrato dell'ipotenusa.

il triangolo rettangolo del teorema di Pitagora e' qualsiasi, sono infiniti triangoli rettangoli, non c'e' legame tra loro (se non l'angolo retto), sono una folla sregolata; come averne una visione?

Occorre organizzare! Sempre sulla base delle ricevute info scolastiche, pero' tra loro isolate; e' un tipo di insegnamento "puntiforme", in cui, se va bene,

• nei manuali si ritrovano le risposte a domande che non si sa neppure siano esistite

domande che pero' danno la connessione di rete di conoscenze (conoscenza) e la storia.

La famiglia di forme dei triangoli rettangoli, elencati con continuita'

Triangolo rettangolo,
inscritto in una circonferenza,
il vertice retto mobile la percorre.

Ho fermato l'animazione li' perche' il resto lo posso immaginare-dedurre per simmetria.
Sono TUTTE le forme simili possibili di triangolo rettangolo, generate dal moto di deformazione continua-differenziabile della configurazione.

Mentre manipolo la creta o l'impasto di farina, ecc ... da bimbo mi formo l'idea di deformazioni continue, volume, e conservazione del volume in tali trasformazioni.

Mentre spargo e smuovo la sabbia o i bottoni sul tavolo, ecc ... mi formo l'idea di deforrmazioni continue, area, densita' areica, e conservazione dell'area in tali trasformazioni.

Osservare l'animazione suggerisce fatti e domande

1) all'occhio sembra:

• cateto corto s'allunga, cateto lungo s'accorcia
• un quadrato cresce, l'altro decresce

in accordo con Q=L², L e Q variabili concordi.

Le lunghezze dei cateti sono variabili discordi,

le aree dei quadrati sono variabili discordi.

2) Domanda generale sulle variabili discordi

accettato che 2 variabili sono discordi, si compensano?

cioe' una aumenta quanto l'altra diminuisce?

equi: la loro somma e' costante?

Nel caso in questione

1. la somma dei quadrati e' costante?
2. la somma dei cateti e' costante?

nm:  a b c, x y z  lunghezza di: cateto cateto ipotenusa;

da db dc, dx dy dz  differenziali di  a b c, x y z.

Corollario al teoPit:
la somma dei quadrati dei cateteti e' cost,
se l'ipotenusa e' cost.

⇒ le variazioni di area dei q sui cateti sono opposte (es -5 +5). (A1)

Detto nella lingua-pensiero dei numeri assoluti:

Variazioni d'area uguaii, opposte in verso,
cioe' una in diminuire, l'altra in aumentare.

1. La variazione di lunghezza dei cateti
   • provoca nei loro quadrati
     variazioni di area opposte.
2. Le variazioni dei cateti non possono essere qualsiasi, poiche' devono provocare variazioni d'area opposte.
   Quali sono le variazioni del cateti? Calcolarle.

Approfond Quadrati equivariano d'area ⇔ R(da,db) ?

"Somma dei quadrati costante" e' circa il teo di Pitagora.

anzi lo e', dato che:

quando un cateto cresce fino all'ipotenusa, il suo quadrato

1. tende al quadrato dell'ipotenusa
2. e  alla somma dei quadrati

che risultano uguali. (unicita' del limite).

Didattica

Dirlo

1. La variazione di lunghezza dei cateti
   • provoca nei loro quadrati
     variazioni di area opposte.
2. Le variazioni di lunghezza dei cateti
   devono essere tali da produrre variazioni d'area dei loro quadrati, opposte

Approfond

A1

Nel calcolo differenziale delle variabili

Teo:  x+y = k  ⇔  dx+dy = 0

Talk

dim: rem1: teo Pitagora: q1 + q2 = q3.

rem2: teo differenziale delle variabili:  
a) d(x+y) = dx + dy    b)  dx_cost = 0. 

dq1 + dq2 = dq3   rem2a

Qui q3=cost poiche' ipotenusa cost.

dq1 + dq2 = 0

dim: rem: teo Pitagora: qa + qb = qc.

rem: teo differenziale delle variabili:   x+y = cost  ⇔   dx = -dy   

Qui  qc = cost  poiche' ipotenusa cost, quindi  dqa = -dqb

Migliorabile, in parte parziale-errato

cmt: il triangolo rettangolo del teorema di Pitagora e' qualsiasi, se ne prendo 2 a caso, non c'e' legame tra loro, e' un "oggetto" in una modalita' inusuale nella vita quotidiana, dove gli oggetti o sono rigidi o sono deformabili. Cosicché con le trasformazioni continue-differenziabili mi formo l'idea della possibile conservazione del volume della creta o dell'impasto della farina mentre li manipolo.