
- togliendo un quadrato, rimane un rettangolo simile.
E' una forma di autosimilarità.
 |
Rettangolo aureo (=def)
E' una forma di autosimilarità. |
Rapporto aureo golden ratio sezione aurea proporzione aurea
(=def) il rapporto tra lato lungo e corto del rettangolo aureo: 1,618...
fa un nuovo rettangolo.
Ambientando questa corrispondenza nell'insieme dei rettangoli, si definisce un'applicazione all'interno dell'insieme dei rettangoli.
Caso particolare: se si parte da un quadrato, togliendo un quadrato si toglie tutto, cosa rimane? non rimane piu' nulla.
Sottrarre si puo' solo sul fianco del lato corto (un quadrato di lato corto), e cio' acccorcia il lato lungo.
Aggiungere si puo' su entrambi i lati.
Aggiungere a fianco del lato corto e' banale, poiche' non fa altro che allungare il rettangolo (il suo lato lungo).
Costruire un rettangolo da un rettangolo, accostando al lato maggiore un quadrato di pari lato.
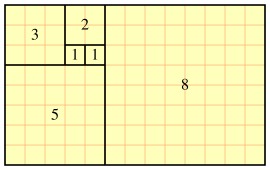 |
Successione di Fibonacci e' quando si parte da un quadrato, e si aggiunge; e' la successione delle lunghezze dei lati dei quadrati. 1 1 2 3 5 8 13 21 34 ... |
|
 |
Rettangolo aureo (=def)
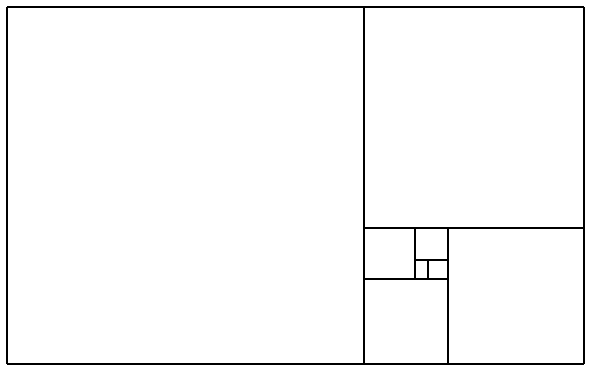
Il procedimento si puo' ripetere sul rettangolo ottenuto: |
|
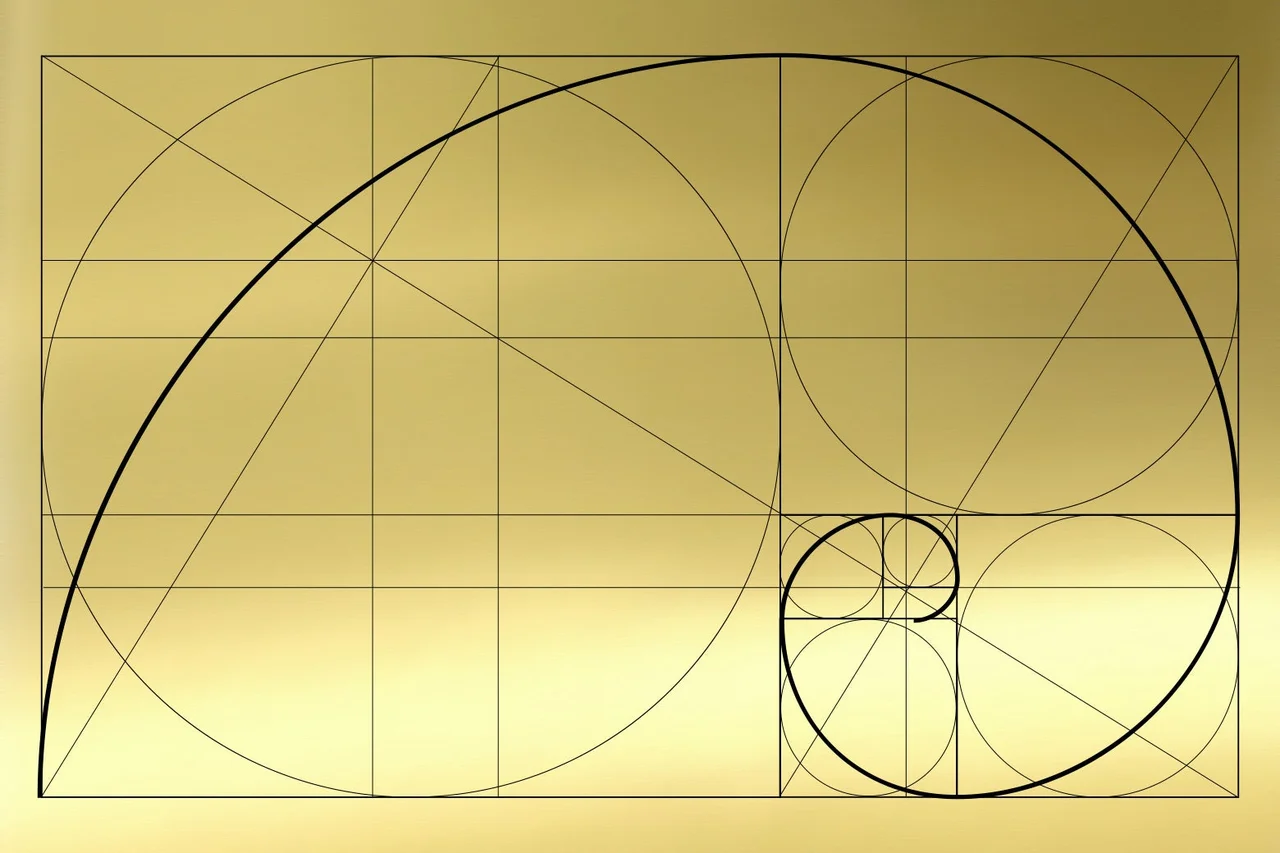
| si puo' fare una spirale |
|
rappresentiamo un rettangolo come coppia delle lunghezze dei lati (L1,L2)
(15, 12) (3, 12) (3, 9) (3, 6) (3,3)
(15, 10) (5, 10) (5, 5)
(21, 34) (21, 13) (8, 13) (8, 5) (3, 5) (3, 2) (1, 2) (1, 1)
partendo da una coppia consecutiva di nr della sequenza di Fibonacci, si resta nella sequenza.
D: quando si arresta la sequenza in sottrazione ?
R: quando arriva ad un quadrato.
rettang_aureo_1.ggb |1b|2|3|4|4_nolabel
rettang_simil_intern_estern.ggb
golden ratio
La mia esplorazione e' iniziata prima con un pezzo di carta, cercando di trovare una costruzione adatta all'uso di GG per quanto lo conoscevo. A posteriori dello studio, ho dovuto imparare piu' di quanto sapessi, per poter fare i disegni che volevo.
Le prime costruzioni erano centrate sul rettangolo e sull'aggiunta del quadrato, ma dopo 3 o 4 tentativi il quadrato mi ha preso la mano, ed e' diventato il personaggio principale.
x(A) coordinata x di un punto. Non xA come avevo tentato di fare, prima di riuscire a scovarla nell'help: Pre-defined Functions and Operations. E' una funzione. Nel linguaggio insiemistico e' la funzione proiezione (dello spazio prodotto, in uno degli spazi fattore).
In uno spazio euclideo si usano riferimenti che sono le figure che uno traccia; e' un riferimento relativo. Non c'e' un riferimento standard come nel piano cartesiano. Ma dove disegnare il primo punto o la prima retta? Posso disegnarlo a caso, e allora e' un punto libero, oppure posso presupporre che nel mio piano euclideo ho cmq 2 assi di riferimento di comodita', in pratica per visualizzare sullo schermo (clid-dx sullo schermo > Vista Standard). Quindi se non mi serve che il primo punto sia da portare a spasso, lo posso fissare nell'origine (GG: Intersect[xAxis, yAxis]), o su uno degli assi.
Ho riscoperto la serie di Fibonacci: e' quando si parte da un rettangolo quadrato.