__________
/ / / Parallel-ogrammi 2D
/____/____/ -epipedi 3D
/ / /
/____/____/ figura auto-simile

Progressione geometrica di figure.
__________
/ / / Parallel-ogrammi 2D
/____/____/ -epipedi 3D
/ / /
/____/____/ figura auto-simile
|
|
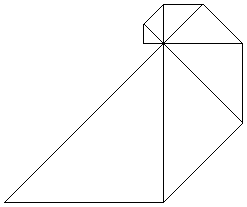 |
ref: Triangolo rettangolo meta' del quadrato. |
 questo esagono e' autosimile ?
questo esagono e' autosimile ?
wp/Self-similarity | wp/Auto_similarità
sarebbe il termine piu' regolare poiche' deriva da "similitudine", che e' il concetto su cui il significato si basa.
"Autosimilarità" e' qiuello che ho visto usato in wp.
"Autosimiglianza" e' quello che mi veniva spontaneo prima di aver visto "autosimilarità", e devo riconoscere che "simiglianza" non e' "similitudine", ma neanche "similarità" lo e'.
 |
|
 |
|
 |
|
La progressione della figura autosimile.
from The Algorithmic Beauty of Plants
The notion of symmetry is generally defined as the invariance of a configuration of elements under a group of automorphic transformations. Commonly considered transformations are congruences, which can be obtained by composing rotations, reflections and translations.
Could we extend this list of transformations to similarities, and consider selfsimilarity as a special case of symmetry involving scaling operations?
On the surface, this seems possible. For example,
Weyl [159, page 68] suggests: “In dealing with potentially infinite patterns like band ornaments or with infinite groups, the operation under which a pattern is invariant is not of necessity a congruence but could be a similarity.”
The spiral shapes of the shells Turritella duplicata and Nautilus are given as examples. However, all similarities involved have the same fixed point. The situation changes dramatically when similarities with different fixed points are considered. For example, the Sierpinski gasket is mapped onto itself by a set of three contractions T1, T2 and T3 (Figure 8.1a). Each contraction takes the entire figure into one of its three main components. Thus, if A is an arbitrary point of the gasket, and T = Ti1Ti2 . . . Tin is an arbitrary composition of transformations T1, T2 and T3, the image T(A) will belong to the set A. On the other hand, if the inverses of transformations T1, T2 and T3 can also be included in the composition, one obtains points that do not belong to the set A nor its infinite extension (Figure 8.1b). This indicates that the set of transformations that maps A into itself forms a semigroup generated by T1, T2 and T3, but does not form a group.
Thus, self-similarity is a weaker property than symmetry, yet it still provides a valuable insight into the relationships between the elements of a structure.