^^Teo: Le mediane si incrociano tutte in 1 unico punto. dim ricorsiva

ix

In generale 3 rette si intersecano a vicenda in 3 punti

e' per questo che occorre dimostrare che le mediane si incontrano in 1 unico punto.

dim:

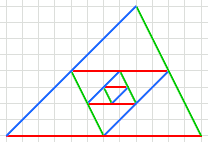E' una dim direi ricorsiva.

Mi domando se sarebbe stata accettata ai tempi di Euclide.

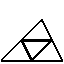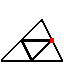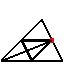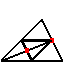
Ripetendo la costruzione del trilato dei punti medi, detto breve informale:

  1. il trilato diventa sempre piu' piccolo
  2. il punto di intersezione di 2 mediane di un trilato e' anche il punto di intersezione delle mediane del trilato seguente
    ⇒ e' punto di intersezione di tutti i trilati
  3. questi punti di intersezione, 3 potenzialmente distinti, al procedere della successione risultano sempre piu' vicini a causa del rimpicciolimento del trilato, fino a risultare 1 solo punto = all'intersezione dei trilati.

Avviso al lettore

fino a qui la lettura "piacevole", e mi sembra credibile, ma se si vuole puntualizzare fino in fondo prosegue nell'approfondimento, ma diventa impegnativo e vale la pena solo se si ha un interesse specifico  :-)

Piu' oltre, nel diario, spiego come sono arrivato all'idea.

Links

Ricorsione matematica. Definizione ricorsiva. Struttura ricorsiva. Induzione matematica.

 

Approfondimento

Precisando (ma ho ancora qualche dubbio):

dim2: Teo: La mediana di un trilato e' anche mediana del trilato dei punti medi, nella meta' lontana dal vertice.

⇒ per induzione, la mediana del trilato seguente e' contenuto nella mediana dell'attuale.
E: l'intersezione di 2 mediane e' interna al trilato poiche' lo sono le mediane.

E: l'intersezione di 2 mediane e' interna al trilato dei punti medi poiche' ... altrimenti le 2 mediane avrebbero 2 intersezioni distinte: una dentro e una fuori il tri dei punti medi.

dim3: Teo: una successione annidata di insiemi il cui diametro → 0, ha intersezione al massimo di 1 punto. es: successione intervalli [0,1/n]∩=0 ma non (0,1/n) che ha intersezione vuota.

Teo: La mediana di un trilato e' anche mediana del trilato dei punti medi, nella metà lontana dal vertice. >>>

 

Diario

Mi era sorto l'interesse per i centri dei trilati, poiche'

i centri dei trilati si assomigliano:

sono associati a 3 segmenti,

Trovai allora su Wikipedia una definizione generale di centro di un triangolo (wp/Punti_notevoli_di_un_triangolo), ora (28-9-2019) ho trovato come sono chiamati i segmenti (wp/Ceviana).

Che i 3 segmenti si incontrino in 1 solo punto, e' facile dimostrarlo per gli assi e le bisettrici; con suggerimento di AndreaFarusi ero riuscito con le altezze, mi mancavano le mediane. Sempre i centri mi avevano sottolineato l'importanza dei punti medi dei lati del trilato, e qui ho "battezzato il trilato dei punti medi", e

 

il trilato dei punti medi mi ha portato a pensare alla loro successione (poiche' la genesi e il generare serie geometriche mi e' sempre piaciuto e interessato)

  

, e qui mi si e' accesa l'idea per la dimostrazione.

 

 

 

Talk

 

Diario (versione discorsiva)

Mi era sorto l'interesse per i centri dei triangoli, poiche' si assomigliano: associati a 3 segmenti che incrociano in un unico punto, detto "centro".

Trovai allora su Wikipedia una definizione generale di centro di un triangolo (wp/Punti_notevoli_di_un_triangolo), ora (28-9-2019) ho trovato come sono chiamati i segmenti (wp/Ceviana).

Che i 3 segmenti si incontrino in 1 solo punto, e' facile dimostrarlo per gli assi e le bisettrici, con suggerimento di AndreaFarusi ero riuscito con le altezze, mi mancavano le mediane.

 

Versioni

dim:

ripetendo la costruzione del trilato dei punti medi

  1. il trilato diventa sempre piu' piccolo, e cosi' anche le mediane
  2. consideriamo la successione dei trilati e le 3 successioni delle mediane:
  3. ognuna di queste successioni annidate converge ad 1 punto = all'intersezione dei propri elementi
  4. l'intersezione dei trilati contiene ognuna delle intersezioni delle mediane

    ⇒  i punti limite coincidono

dim2: Teo: La mediana di un trilato e' anche mediana del trilato dei punti medi (per meta').

⇒ per induzione, la mediana del trilato seguente e' contenuto nella mediana dell'attuale.

dim3: Teo: una successione annidata di insiemi chiusi (in senso topologico) il cui diametro → 0, ha intersezione = 1 punto. es: successione intervalli [0,1/n), ma non (0,1/n) che e' vuota.

 

dim:

ripetendo la costruzione del trilato dei punti medi, in breve informale:

  1. il trilato diventa sempre piu' piccolo
  2. il punto di intersezione di 2 mediane di un trilato e' anche il punto di intersezione delle mediane del trilato seguente
  3. questi punti di intersezione, 3 potenzialmente distinti, al procedere della successione diventano sempre piu' vicini a causa del rimpicciolimento del trilato, fino a convergere ad 1 solo punto = all'intersezione dei trilati.

Precisando:

dim2: Teo: La mediana di un trilato e' anche mediana del trilato dei punti medi, nella meta' lontana dal vertice.

⇒ per induzione, la mediana del trilato seguente e' contenuto nella mediana dell'attuale.
E: l'intersezione di 2 mediane e' interna al trilato poiche' lo sono le mediane.

dim3: Teo: una successione annidata di insiemi chiusi (in senso topologico) il cui diametro → 0, ha intersezione = 1 punto. es: successione intervalli [0,1/n]∩=0 ma non (0,1/n) che ha intersezione vuota.