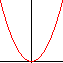
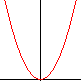
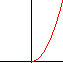
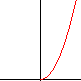
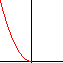
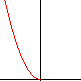
NON proporzionali a x
y=kx
y=kx+y0
y0≠0
≡kx1/2
proporzion
inversa
sce
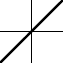
k>0
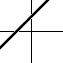
k>0
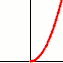
x≥0 e k>0
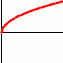
k>0
cre
sce

k<0
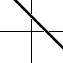
k<0
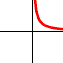
x>0 e k>0
/costante / pendenza costante
/ /crescente - pendenza crescente
\ mono-tonica \ pendenza decrescente
\ / \decrescente
variabile
\ /periodica
bi-tonica
\aperiodica
Prosegue^^
| Proporzionali |
NON proporzionali a x |
||||
|---|---|---|---|---|---|
| proporzione y=kx |
uniforme y=kx+y0 y0≠0 |
y=kx2 | y=k√x
≡kx1/2 |
y=k(1/x) proporzion inversa |
|
| cre sce |
 k>0 |
 k>0 |
 x≥0 e k>0 |
 k>0
|
|
| de cre sce |
 k<0 |
 k<0 |
|
|
 x>0 e k>0 |
Schema max
| V A R I A B I L I |
scollegate | variabili concordi ↔ funzione crescente |
||||||
|---|---|---|---|---|---|---|---|---|
| collegate y=k
|
||||||||
| collegate y≠k |
Proporzionali |
NON proporzionali |
||||||
| proporzione y=kx |
uniforme y=kx+y0 y0≠0 |
y=kx2 | y=kx1/2
≡k√x |
y=k(1/x) proporzion inversa |
||||
| M |
cresce |
 k>0 |
k>0 |
 o k>0 e x≥0
o k<0 e x≤0 |
 k>0 |
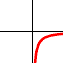 x>0 e k<0
x<0 e k<0 |
||
|
de- cresce |
 k<0
|
 k<0
|
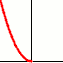 o k>0 e x≤0
o k<0 e x≥0 |
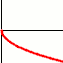 k<0 |
 x>0 e k>0
x<0 e k>0 |
|||
| B I T O N E |
oscilla | no | no |
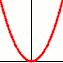 k>0
k<0
aperiodica |
no |
k>0
k<0 aperiodica |
||
pendenza
| y=ax2+bx+c | |
|---|---|
| cresce | a>0 e x≥(-b/(2a)) a<0 e x≤(-b/(2a)) |
| decresce | a>0 e x≤(-b/(2a)) a<0 e x≥(-b/(2a)) |
 tratto costante
tratto costante
-o: costante di livello
-o: costante di diminuzione, o aumento
| Dunchi | lo schema ideale di uno scivolamento si puo' rappresentare con un grafico costante di diminuzione di energia; quindi verrebbe fuori una scaletta decrescente. |
|---|
Oltre i grafici senza scala con il solo grafico, puo' essere utile evidenziare 3 punti sul grafico a variazione orizzontale costante, in modo da evidenziare la corrispondente variazione verticale.
Siccome la principale rappresentazione degli andamenti e' tramite il piano cartesiano, le stesse espressioni sono usate per i diagrammi.
| 130 | Tipi di andamento di una corrispondenza: | 3 | |
| - concorde, o crescente | 1 | ||
| - discorde, o decrescente | 1 | ||
| - costante | 1 |
/ pendenza costante
/costante /crescente - pendenza crescente
\ mono-tonica \ pendenza decrescente
\ / \decrescente
variabile
\ /periodica
bi-tonica
\aperiodica
| V A R I A B I L I |
scollegate y=k |
|||||
|---|---|---|---|---|---|---|
| collegate y≠k |
Proporzionali |
NON proporzionali |
||||
| proporzione y=kx |
uniforme y=kx+y0 y0≠0 |
y=kx2 | y=kx1/2
≡k√x |
y=k(1/x) | ||
| concordi | k>0 | k>0 | o k>0 e x≥0 o k<0 e x≤0 |
k>0 | k<0 | |
| discordi | k<0 | k<0 | o k>0 e x≤0 o k<0 e x≥0 |
k<0 | k>0 | |
| oscillanti | mai | mai | mai | mai | ||
| V A R I A B I L I |
scollegate | ||||||
|---|---|---|---|---|---|---|---|
| collegate | |||||||
| proporzione y=kx |
uniforme y=kx+y0 |
y=kx2 | y=kx1/2
≡k√x |
y=ax2+bx+c | |||
| concordi | k>0 | k>0 | o k>0 e x≥0 o k<0 e x≤0 |
a>0 e x≥(-b/(2a)) | |||
| discordi | k<0 | k<0 | o k>0 e x≤0 o k<0 e x≥0 |
||||
| oscillanti | mai | mai |
| V A R I A B I L I |
scollegate | s | s | s | s | s | s | s |
|---|---|---|---|---|---|---|---|---|
| collegate y=k
|
s | s | s | s | s | s | s | |
| collegate y≠k |
Proporzionali |
NON proporzionali |
||||||
| proporzione y=kx |
uniforme y=kx+y0 y0≠0 |
y=kx2 | y=kx1/2
≡k√x |
y=k(1/x) proporzion inversa |
||||
| M |
var concordi funz crescente pendenza
|
 k>0 |
 k>0 |
 o k>0 e x≥0
o k<0 e x≤0 |
 k>0 |
 x>0 e k<0
x<0 e k<0 |
||
| var discordi funz decrescente pendenza
|
 k<0
|
 k<0
|
 o k>0 e x≤0
o k<0 e x≥0 |
 k<0 |
 x>0 e k>0
x<0 e k>0 |
|||
| B I T O N E |
oscillanti
|
no | no |
 k>0
k<0
aperiodica |
no |
 k>0
k<0 aperiodica |
||