^^Pythagorean theorem, Newton style.

Presentazione  >>>

motivazioni dell'autore; ambiente del teo(rema); opinioni sull'educazione scientifica.

• Si puo' leggere prima, dopo, o no, della dim(ostrazione) del teo, che segue qui sotto;
  • per capire e' sufficiente una competenza di base del calcolo infinitesimale.

La famiglia di forme dei triangoli rettangolo, elencati con continuita'

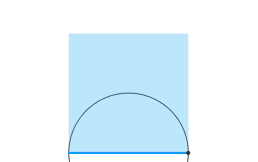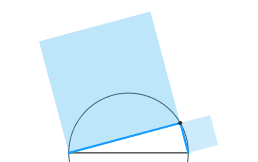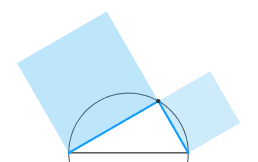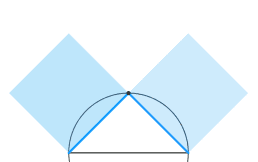
Triangolo rettangolo,
inscritto in una circonferenza,
il vertice retto mobile la percorre.

Ho fermato l'animazione li' perche' il resto lo posso immaginare-dedurre per simmetria.
Sono TUTTE le forme simili possibili di triangolo rettangolo, generate dal moto di deformazione continua-differenziabile della configurazione.

nm:  a b c, x y z  lunghezza di: cateto cateto ipotenusa;

da db dc, dx dy dz  differenziali di  a b c, x y z.

ẋ  ẏ   notazione di Newton per la derivata temporale di x(t) y(t)

a→0   a tende a 0 (zero)

Idea per dimostrare il teo di Pitagora, da sopra stimolata

dimostrare

Teo:  a²+b² = cost,  quando  c = cost

Poi, dato che

• se una variabile costante assume in un caso il valore k,
  allora e' costante a k

per dimostrare teoPit e' sufficiente mostrare che

Teo: a²+b² = c²  in 1 caso

il caso esiste, semplice

tri(angolo) rettangolo isoscele, cioe' meta' q(uadrato) tagliato da diagonale; q cateto  =  doppio tri q diagonale  =   doppio del doppio tri

dim semplice in stile Newton per a²+b² = c², dato a²+b² = k

Se a→0 allora b→c, quindi 

a²+b² →  0²+c²  =  c²     

Essendo per ipotesi la somma costante, il suo limite per a→0 e' tale costante, limite che abbiamo or ora calcolato essere c² !

Teo:  a²+b² = cost,  quando  c = cost

Per indagare, conviene inquadrare la situazione cosi'

• i quadrati variano d'area in ugual misura,
      vincola tra loro da db
• il vertice si muove rimanendo retto
      vincola tra loro da db

Se i vincoli sono stesso vincolo ed e' CNS (Condizione Necessaria e Sufficiente) in entrambi i casi, allora:

• il vertice si muove rimanendo retto, se e solo se
  i quadrati sui cateti variano d'area in ugual misura.

I quadrati equivariano d'area  ⇔  R(da,db) ?

x²+y² = cost      derivando rispetto al tempo entrambi i membri

2xẋ + 2yẏ = 0     semplific div2

xẋ + yẏ = 0

Conclu

Detto con le variazioni assolute

• i quadrati equivariano d'area  ⇔    a*da = b*db

A parole: le variazioni sono inv prop ai valori.

Un approccio elementare figurato e' qui.

Resta da dimostrare

Teo: il vertice si muove rimanendo retto ⇒  a*da = b*db

osservare l'animaz

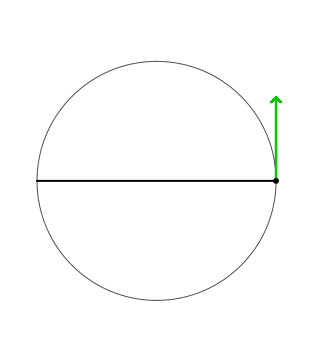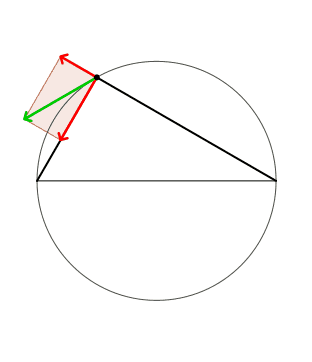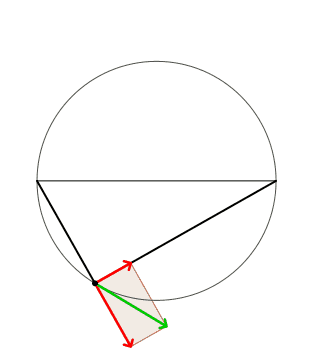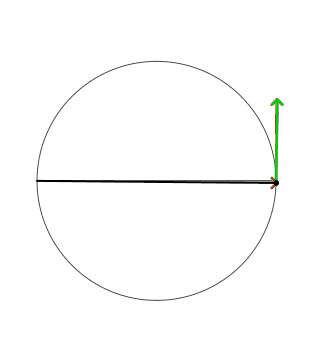
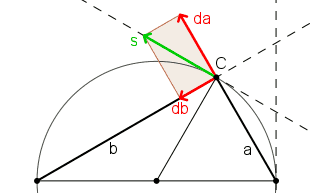
ingranditi 20 volte

s  spostamento del vertice C dell'angolo retto sulla circonferenza

da db  variazione di a e b dovuti a s.

Calcolare la variazione di lunghezza dei cateti

I cateti sono visti come:

segmenti con un capo fisso sul diametro, e un capo mobile
(analoghi al raggio di un sistema di riferimento polare).

Teo: la variazione infinitesima di lunghezza di un raggio polare
= proiezione ortogonale dello spostamento del capo mobile sulla direzione del raggio.

Equi: la velocita' radiale  =  proiezione ortogonale della velocita' del capo mobile sulla direzione del raggio.

Il fatto centrale e':

• le proiezioni dello spostamento hanno triangoli di proiezioni con gli stessi angoli del triangolo mobile

per cui    lato_lungo_A * lato_corto_B  =  lato_corto_A * lato_lungo_B

              a*da = b*db

Links

Velocita' radiale e trasversale.

Talk

https://en.wikipedia.org/wiki/Notation_for_differentiation

Idea per dimostrare il teo di Pitagora, da sopra stimolata

1) dimostrare che  a²+b² = cost  (quando  c = cost)

usando il modo cinetico-infinitesimale !

Detto col calcolo infinitesimale attuale: Derivata di  a²+b² = 0.

2) Poi per dimostrare il teo e' sufficiente mostrare che

a²+b² = c²  in 1 caso; il che esiste, semplice

Giustificazione formale

per: 1) limite della somma = somma dei limiti

       2) limite del prodotto =  prodotto dei limiti

2) lim f()  =  f(lim)   f continua  3)  f(x) := x²  continua

Per indagare conviene inquadrare la situazione cosi'

• somma quadrati = cost, impone una relazione tra da db
• il moto del vertice retto, impone una relazione tra da db

sono la stessa relazione.