^^Reticolo delle mediane.

In generale 3 rette si intersecano a vicenda in 3 punti, e' per questo che occorre dimostrare che le mediane si incontrano in 1 unico punto.

Vogliamo dimostrare logicamente, non solo con un disegno, che

le rette mediane di un tri, disegnate sul reticolo del tri, costituiscono un reticolo di tri.

3 fasci di rette parallele equispaziate non e' detto che siano un reticolo di trilati

infatti:

• 2 fasci di rette parallele equispaziate formano un reticolo di parallelogrammi

ma se la 3 retta e' aggiunta a caso non si forma un reticolo di trilati, affinchè lo sia deve essere una delle 2 diagonali del parallelogramma.

3 dim

1. basata sul reticolo
2. geometria affine
3. Teo: Le mediane si incrociano tutte in 1 unico punto.
   Teo: le rette mediane sono un reticolo di tri ⇔ le mediane di un tri si incrontrano in 1 punto

In un reticolo di tri

1. in un reticolo di tri, togliendo un fascio di rette, rimane un reticolo di parallelogrammi, ma i nodi del reticolo non sono diminuiti, restano inalterati.
2. le rette si incrociano sempre tutte e 3 assieme

Teo: i nodi del reticolo di tri sono "allineati":

1. se da un nodo si passa ad un altro, allora con lo stesso spostamento si arriva ad un altro nodo
2. equi. ogni punto del reticolo fa da centro: ogni punto ha il suo opposto rispetto al centro
3. equi: ogni punto ha il suo opposto rispetto ad un altro.

Def equivalente di Mediana di un trilato (=def)  la semidiagonale del parallelogramma costruito sui 2 lati del suo vertice. Perche' questa def? si adatta al reticolo dei trilati

Dimostrazione di geometria affine

Ambientiamo il trilato nel suo reticolo generato.

In fig in rosso il reticolo delle mediane.

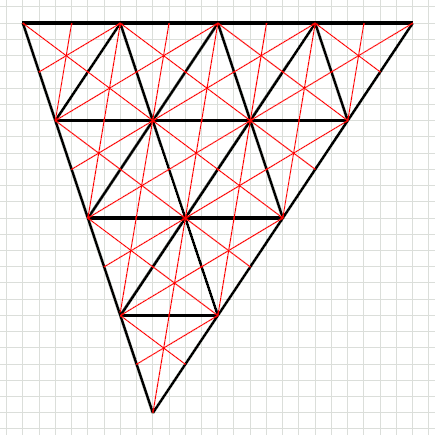Trasformazione affine , Geometria affine   le rette parallele si trasformano in rette parallele (⇒ i punti di incidenza sono mantenuti)   &   segmenti uguali su rette parallele, restano uguali sulle trasformate.

Da

1. Un reticolo di trilati uguali puo' deformare-trasformare con una trasformazione affine nel reticolo di un qualsiasi trilato.
2. Le mediane restano mediane (dim: uniscono 2 punti del reticolo)
3. Le mediane di un tri isoscele si incontrano in 1 solo punto

⇒ le mediane si incontrano in 1 solo punto per un qualsiasi trilato.

Links

1. Mediana di un trilato, baricentro.
2. Tri reticolo.
3. Reticolo delle diagonali, di un reticolo di parallelogrammi.
4. Tassellatura, reticolo, cristallo.