^^Quadrato coi vertici sui nodi della quadrettatura.

Dis quadrato coi vertici sui nodi della quadrettatura.

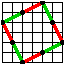
1 .odg|pdf Dis quadrato coi vertici sui nodi della quadrettatura.
2 .odg|pdf Tutte le inclinazioni.
3 .odg|pdf Dis una figura con il bordo fatto da rettangoli congruenti (rettangoli coi lati sulla quadrettatura). Propedeutico n. 1 a "Dis quadrato coi vertici sui nodi".
4 .odg|pdf Dis un quadrato con il bordo quadrato fatto da 4 rettangoli congruenti (rettangoli coi lati sulla quadrettatura). Propedeutico n. 2.
5 .odg|pdf Angolo, triangolo, rettangolo.  Propedeutico n. 3.
6 .odg|pdf Studio. Scientifico e artistico.
7 .odg|pdf Dis un quadrato inclinato partendo dalla sua scatola.

Esito della proposta in classe

In 1c_iti_2012 e' stato proposto 1, ma solo 3 allievi sono riusciti a disegnare i quadrati inclinati. Che fare? La prima cosa che viene in mente e': Occorre fare un esercizio propedeutico.

Il primo disegno propedeutico che mi viene in mente e': inscatolare i segmenti inclinati, e di conseguenza, il disegno "sequenza di rettangoli consecutivi che si piegano a quadrato", in altre parole Quadrato e rettangoli. Sviluppo l'idea 3 4 5, ma alla fine non mi soddisfa, poiche' richiede un impegno superiore a cio' che si vuole ottenere.

Occorre trovare altro.

  1. Rotola rettangolo su retta.
  2. Scatola di una figura.
  3. Rotazione di 1/4 giro di un rettangolo e di un segmento

La scatola di un quadrato inclinato e' un quadrato

Disegnare un quadrato inclinato a partire dalla sua scatola.

Dida

  1. "Disegnare un quadrato coi vertici sui nodi della quadrettatura" si puo' vedere come parte di un percorso piu' ampio di Controllare l'inclinazione usando la quadrettatura.
  2. Disegnando, ricordiamoci sempre l'interpretazione cinetica delle linee.
  3. Le enumerazioni, es "Dis TUTTI i casi", "TUTTE le combinazioni", e' un esercizio importante per i piu' dotati e pazienti. Richiede applicazione, per cui anche se semplice, gli studenti che non riescono a mantenere l'attenizione, sono in difficolta'.
  4. Ricopiare. Il ruolo del "ricopiare" nel disegno. Analogo al "disegno dal vero".
    "Ricopiare il disegno" vs "disegno descritto a parole".

Alter

Tutte le inclinazioni.

Dis TUTTI i quadrati inclinati, coi vertici sui nodi.
Combinando componenti orizzontale e verticale dell'inclinazione.

Quadrati di Tutte le possibili inclinazioni.

Links

  1. Fratello di: Rettangolo coi vertici sui nodi della quadrettatura.
  2. esof: Controllare l'inclinazione usando la quadrettatura.
  3. esof: Quadrettatura. Griglia. Ambiente. Usare la quadrettatura.

Disegno

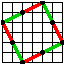
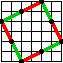
La differenza sta solo nel bordo. Inizialmente di 2 px, ma questo porta a una dimensione di 65px, che ora (gen2012) che tenderei alle icone 64x64 e' fuori scala di di 1 pixel, quindi ho studiato come viene con il margine left-top 2px e gli opposti di 1 pixel, poi tutto di 1px. Credo di usare la 63x63 la piu' piccola, margine uniforme di 1px.