^^c: Calc HfA con la formula H= R - √(R² - A²), e compilare tb. 

 tx | dis | par | E | frml | Efrml | tb | grf | arrot | crc | ½x²

I valori da usare in tb. UM=cm

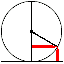
R=10;  A= 0 1 2 3 ... 10.

Chi vuole puo' usare il foglio di calcolo.  .ods

Es di calcolo dell'espressione, con indicazione e sviluppo con tutti i singoli passaggi

Rem: Scrittura in riga della radice quadrata.

A =3  

A

 =4
H = R - √(R² - A²)

= 10 - √(10² - 3²)

= 10 - √(100-9)

= 10 - √91

= 10 - 9,54

= 0,46

= 0,5

        H = R - √(R² - A²)

= 10 - √(10² - 4²)

= 10 - √(100-16)

= 10 - √84

= 10 - 9,17

= 0,83

= 0,8

2 possibilita': () Solo risultato.  () Scrivere i passaggi.

() Solo risultato.

x≡A cA=  √(R² - A²) y≡H= R - cA y
0 10 0 0
1 9,95 0,05 0,05
2 9,80 0,20 0,2
3 9,54 0,46 0,5
4 9,17 0,83 0,8
5 8,66 1,34 1,3
6 8 2 2
7 7,14 2,86 2,9
8 6 4 4
9 4,36 5,64 5,6
10 0 10 10

() Scrivere i passaggi. Sostituzione e sviluppo dell'espressione numerica.

Per verificare che tutti sappiamo come sostituire i numeri alle lettere.

R=10  A= 0 1 2 3 ... 10

Per economia (anche futura), spezziamo il calcolo, calcolando come dato intermedio ...
il cateto complementare (co-cateto cocateto)  cA =  √(R² - A²)

Compilare anche i casi A=0 e A=1.

Sono casi particolari, il cui risultato si conosce ad occhio osservando il caso nella figura, ed e' importante rendersi conto che la formula funziona anche per essi.

 

Guida ins

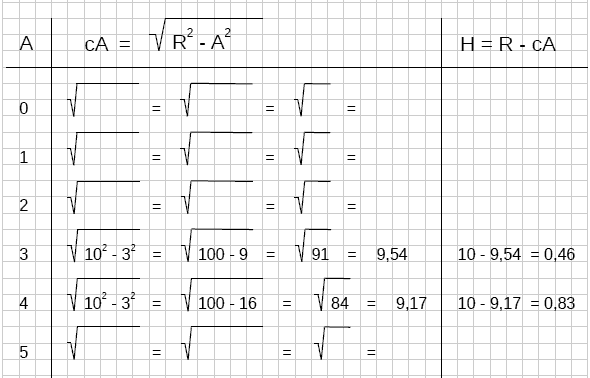
Arrivo: Altezza del pendolo calcolata col teo di Pitagora, dall'ampiezza.

Poi: HfA grf.

brother: Approssimare risultato.

Scrittura in riga della radice quadrata.

Si presenta il Trilato pitagorico 6 8 10, doppio di 3 4 5.

L'esercizio ha 2 aspetti

L'ho assegnato come "calc expr", ma poi ho visto che non c'era uniformita' nelle cifre decimali, questo anche perche' il contesto era lasciato implicito, e poteva essere:

Disegno tabella con radice quadre standard .odg|pdf zoom 75%

Come impostare la tabella ?

Dopo aver oscillato, credo sia meglio quella orientata allo sviluppo,

Privilegia lo sviluppo del calcolo

x≡A cA=  √(R² - A²) y≡H= R - cA
0    
1    
2    
3 √(10² - 3²) = √(100-9) = √91 = 9,54 10 - 9,54 = 0,46
4 √(10² - 4²) = √(100-16) = √84 = 9,17 0,83 - 9,17 = 0,83
5    
6    
7    
8    
9    
10    

Compromesso tra sviluppo ed evidenziare il risultato

Il compromesso e' necessario altrimenti tb troppo larga

x≡A cA=  √(R² - A²) cA y≡H= R - cA
0      
1      
2      
3 √(10² - 3²) = √(100-9) = √91 = 9,54 0,46
4 √(10² - 4²) = √(100-16) = √84 = 9,17 0,83
5      
6      
7      
8      
9      
10      

 

 

 

 

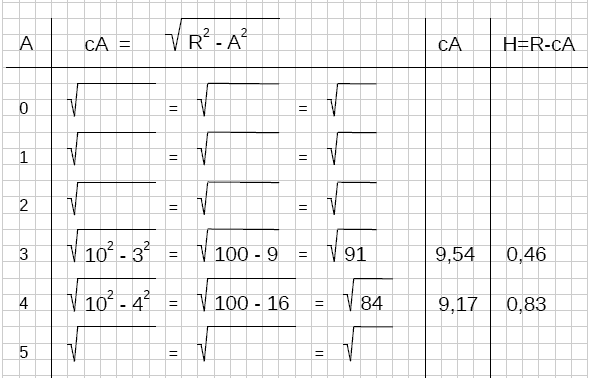
A=3:  H = 10 - √(10² - 3²)

= 10 - √(100-9)

= 10 - √91

= 10 - 9,54

= 0,46

 
A=4:  H = 10 - √(10² - 4²)

= 10 - √(100-16)

= 10 - √84

= 10 - 9,17

= 0,83