^^Altezza osci pendolo,
calc dall'ampiezza, col teo di Pitagora.
p: L'ampiezza dell'osci ne determina l'altezza; come calcolarla ?
Pre: Ampiezza e altezza del pendolo; A H osci. Lab. Ini.
Rappresentare per comprendere.
1.
Il corpo pendolare disegnato come un grosso punto, attira troppo l'attenzione e
la distoglie dal quadro generale. Disegnare solo il raggio di rotazione, o un
piccolo punto.2.
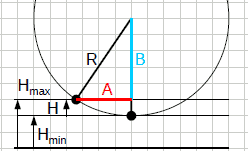
Aggiungere lettere aiuta.
Nome della lunghezza del filo
| R |
raggio di rotazione del pendolo, raggio della traiettoria
circolare |
Paragonare per comprendere >>>
Dialogo socratico. Spiega con aiuti
.odg|pdf
| classe |
si (1E 2015 16-10) |
|
tutti dicono di conoscerlo, adesso vediamo se lo sapete applicare. |
| Bragazzi |
√(A² + R²) |
|
No. Guardiamo meglio il triangolo cui applichiamo il teo di Pitagora.
Aiuto 1 |
| Pepa |
√(R² - A²) |
|
No |
| Nardini |
H = √(R² - A²) |
| |
No. Aiuto 2 |
| Mancolli |
H = R - A |
|
No, sottrazione diretta di segmenti |
| |
√(A² - R²) |
|
No, impossibile poiche' A < R. Aiuto n. 3. |
| |
sottrarre a R, √(R² - A²) |
| |
Si, ma queste parole trasformiamole in una espressione matematica |
| classe |
H = R - √(R² - A²) |
Links
- Pre: Ampiezza e altezza del pendolo; A H osci. Lab. Ini.
che e' un pre comune anche ad un altro possibile prePre:
Ampiezza e
altezza di un'osci del pendolo.
- Altezza del pendolo.
- Pitagora; teorema.
- Uso: Velocita' all'estremo
inferiore, ms cronometro 1 fotocellula.
-
Approfond
Guida ins
Giustificazione dell'argomento che sembra un fare per il fare, senza uno
scopo preciso
- applicazione del teoPitagora
- completare la conoscenza della configurazione a partire dai dati che la
determinano.
Non necessariamente ci deve essere uno scopo, che e' legato all'utilita', e'
utile anche stimolare la curiosita', fare per curiosita', che e' legata al
piacere della conoscenza.
Rappresentazione del corpo pendolare
- il corpo pendolare e' disegnato non piu' come un grosso punto, bensi'
come gli altri
- il corpo pendolare non e' disegnato
- il corpo pendolare e' il punto estremo del raggio di rotazione.
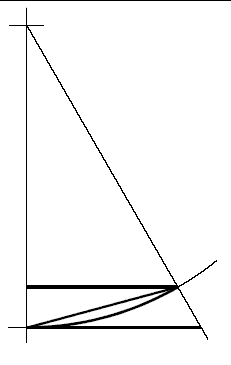
c: Compila una tb x y che calcoli con la formula inventata. R=10.
x=A= 0 1 2 3 ... 10 y=H. Scrivere la formula per ognuno dei
valori della x.
La formula scritta con x e y e' y= √R² - x²
c: preferisco siano mentalizzati sul caso concreto, quindi non trasformo
nella formula astratta.
Titolo
- Altezza del pendolo calcolata col teo di Pitagora, dall'ampiezza.
c: originale
- Altezza di un'osci del pendolo, calcolata dall'ampiezza, col teo di
Pitagora.
c: 27-12-2017. Cambiato per effetto domino, da
Ampiezza e altezza di un'oscillazione del pendolo.
Residenza
Originale in ix Pendolo. Tipi di
oscillazione, caratteristiche.
27-12-2017 spostato in ix Leggi del pendolo.
Talk
Rappresentare per comprendere. Il corpo pendolare ...
NomeFile
- pen_alt_pit originale, come abbreviaz di "calc altezza con teo
pitagora"
- pen_amp_alt_per poi, per sensibilizzarmi alla coordinazione di A H
Rappresentare per comprendere.
cmt: rivedendo mi e' sembrato che i 2 cerchi quasi uguali, a parte la
differenza del punto, creino piu' confusione che sostanza