^^Elevazione del pendolo approssimata con una parabola.

 tx | dis | par | E | frml | Efrml | tb | grf | arrot | crc | ½x²

 

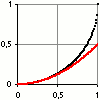
Circonferenza approssimata con una parabola, e' il tema geometrico sottostante a questa realta'

 

  Circonferenza Parabola
osculatrice
R=1 y=1-√(1-x2)

 
y= 1
2		 x2
     
R≠1 y=R-√(R2-x2)

 
y
R		 = 1- √(1-( x
R		 ) 2 )

y
R		 = 1
2		 ( x
R		 ) 2

 

y = x²
2R

 

Elevazione in funzione dell'ampiezza. Approssimazione piccoli angoli.

L'elevazione e' proporzionale al quadrato dell'ampiezza.

es: Se l'ampiezza raddoppia, l'elevazione quadruplica.

mem: Elevazione del pendolo in funzione dell'ampiezza.

L'elevazione e' proporzionale al quadrato dell'ampiezza, nel caso delle piccole oscillazioni.

y = kx2    y = elevazione; x = ampiezza

Spiega: parabola osculatrice della traiettoria circolare.

 

 

Approfond

Formule. Alter espo.

Legenda: x ampiezza, y elevazione.

  R=1 R ≠ 1
Formula esatta: y=1-√(1-x2) y=R-radq(R2-x2)

y/R = 1-radq(1-(x/R)2)
Approssimata
y= 1
2		 x2
y
R		 = 1
2		 ( x
R		 ) 2

Elevazione in funzione dell'elongazione.

L'elevazione dipende dal quadrato dell'elongazione, per piccoli angoli.

Se l'elongazione della piccola oscillazione raddoppia, l'elevazione quadruplica.

 

 

Talk

Titolo

  1. Elevazione in funzione dell'elongazione.
  2. Elevazione del pendolo in funzione dell'ampiezza, approssimata con una parabola.
    c: originale
  3. Elevazione del pendolo approssimata con una parabola.
    c: 28-12-2017 e' come me lo ricordo, un po' piu' stringato dell'originale. In piu' assomiglia al titolo dell'astratto geometrico Circonferenza approssimata con una parabola

Il tema geometrico sottostante a questa realta' e':