










| Set | 15 | 22 | 29 | ||
|---|---|---|---|---|---|
| Ott | 06 | 13 | 20 | 27 | xx |
| Nov | 03 | 10 | 17 | 24 | |
| Dic | 01 | 08 | 15 | 22 | |
| Gen | 05 | 12 | 19 | 26 | |
| Feb | 02 | 09 | 16 | 23 | |
| Mar | 02 | 09 | 16 | 23 | 30 |
| Apr | 06 | PP | 20 | 27 | xx |
| Mag | 04 | 11 | 18 | 25 | |
| Saper|Pat|Mtm|Lib|Rcp | |||||
| 1201 | |
| 1901 |
 |
| 2601 |
 In classe: rotola rett su rett 6x4 su 14x6. Dis, tb pos spost. esp: Misurare 3 forze applicate a un ometto appendiabiti. c: E' stata consegnata una scheda col disegno in scala delle forze, da scomporre. |
| 0202 |
 1
crz Rotola rettangolo su rettangolo. 2
I segni delle coordinate cartesiane e la loro regola di rotazione.. 3
I segni degli spostamenti. 4 LAB: bottiglia forata
da 2 litri, tra-vasa in bottiglia da 0,5 litri. Misurare durata travaso per
3 riempimenti consecutivi. Precisione al secondo. Portare materiale esp a
scuola. Ripetere con approssimazione entro il 10%. e
c: Dis e Tb Posizioni e spostamenti di "rotola rettangolo su rettangolo 6x4 su 18x2". 1
crz Rotola rettangolo su rettangolo. 2
I segni delle coordinate cartesiane e la loro regola di rotazione.. 3
I segni degli spostamenti. 4 LAB: bottiglia forata
da 2 litri, tra-vasa in bottiglia da 0,5 litri. Misurare durata travaso per
3 riempimenti consecutivi. Precisione al secondo. Portare materiale esp a
scuola. Ripetere con approssimazione entro il 10%. e
c: Dis e Tb Posizioni e spostamenti di "rotola rettangolo su rettangolo 6x4 su 18x2". |
| 0902 |
 Lab:
Grafico volume svuotato in funzione della durata di svuotamento. (Le
bottiglie di Conti) Lab:
Grafico volume svuotato in funzione della durata di svuotamento. (Le
bottiglie di Conti) |
| 1602 | |
| 2302 | |
| 0203 |
 Misurare h L t
Misurare h L t |
| 0903 |
 Disegnare il grafico cartesiano L=f(h)
Disegnare il grafico cartesiano L=f(h) |
| 1603 |
 |
| 2303 |
 Tratto cronometrato tramite coppia di fotocellule.
Tratto cronometrato tramite coppia di fotocellule. |
| 3003 | Verifica compito: misura periodo oscillazioni pendolo di diverse lunghezze. |
| 0604 |
|
| 2004 | Siringa. Struttura. | Spiegazione su come svolgere l'esperimento: "Tirare il pistone della siringa a tenuta stagna. Misurare la forza in funzione del volume della camera."| Inizio esperimento. |
| 2704 |
 Pompa a vuoto, campana a vuoto. Siringa a tenuta stagna si espande sotto la campana a vuoto. |
| 0405 | Equilibrio di pesi su un'asta. |
| 1105 |
 3
forze equilibrate parallele. 3
forze equilibrate parallele. |
| 1105 |
 Vasi comunicanti.
Vasi comunicanti. |
| 1805 | Recupero |
| 2505 |
 3
forze parallele su un corpo esteso. Rifatta con punti di applicazione
piu' distanti. 3
forze parallele su un corpo esteso. Rifatta con punti di applicazione
piu' distanti. |
| 8:00 | 8:50 | 9:45 | ||||
|---|---|---|---|---|---|---|
| L | 1C | 1C | 1AT | 1AT | 2C | 2C |
| M | 2AT | 2AT | ||||
| Me | 1AT | 1C | 2C | |||
| G | 2AT | |||||
| V | 2AT | 2AT | 1C | 2C | 1AT | 1AT |
| cm3 | 2,7 cm3 | 27 cm3 | 270 cm3 | ||||
| d= 2,7 | = | = | = | ||||
| g | 1 g | 10 g | 100 g |
1 . 2 . 3 . 4 . 5 . 6 . e . e .
| Dt | Descrizione
|
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 01 | ^^ Settembre 3 Lab 1 2007. | ||||||||||||||||||||||||
| 15
|
Altri possibili argomenti per una prima lezione >>> |
||||||||||||||||||||||||
| 17 | |||||||||||||||||||||||||
| 18 | |||||||||||||||||||||||||
| 02 | ^^ Settembre 4 Lab 1 2007. | ||||||||||||||||||||||||
| 22 | Ordine reticolare; livelli; rappresentazione in verticale e in orizzontale. c: Scrivi un ordine reticolare con l'esempio di peso e altezza di una persona. c: Scrivi l'ordine reticolare coi voti di italiano e matematica dall'8 al 5 compresi. | ||||||||||||||||||||||||
| 24 | Crz ordine reticolare. c: In 1 foglio disegno del reticolo in grande. | c: Triangolo di Tartaglia | c: Fare un contenitore chiuso che affondi lentamente, zavorrandolo chiudendoci 1 solo corpo. Es: vasetto di vetro con 1 sasso. Precis: il vasetto vuoto deve galleggiare. | ||||||||||||||||||||||||
| 25 | Bilancia a ometto; suoi modelli semplificati: centro-fulcro e bracci, leva a bracci non allineati e allineati. Moto dei punti di un corpo. Indice della bilancia automatica. Bilancia idrostatica. | ||||||||||||||||||||||||
| 03 | ^^ Settembre 5 Lab 1 2007. | ||||||||||||||||||||||||
| 29 |
 1 c: Di tutto cio' che e' stato detto, avete 5 minuti per scrivere 1 cosa
chiara. 2 Vocabolario. Invece di "attraverso", meglio "tramite; per mezzo di".
3 Tabella della
misura degli stati della bilancia e della corrispondente inclinazione.
| Inclinazione Im-percepibile. | Bilancia a leva, automatica, di Baroni. | Verifica costruzione bilancia. 1 c: Di tutto cio' che e' stato detto, avete 5 minuti per scrivere 1 cosa
chiara. 2 Vocabolario. Invece di "attraverso", meglio "tramite; per mezzo di".
3 Tabella della
misura degli stati della bilancia e della corrispondente inclinazione.
| Inclinazione Im-percepibile. | Bilancia a leva, automatica, di Baroni. | Verifica costruzione bilancia. |
||||||||||||||||||||||||
| 01 | Patto formativo, o contratto didattico, tra insegnante e allievi. | Calibrare la bilancia a ometto automatica. | ||||||||||||||||||||||||
| 03 | Bilancia ometto automatica, calibrazione. | ||||||||||||||||||||||||
| 04 | ^^ Ottobre 1 Lab 1 2007. | ||||||||||||||||||||||||
| 06 L |
Lab: Galleggiamento: misure di massa e volume dei corpi, da relazionare al loro galleggiare o non. | ||||||||||||||||||||||||
| 08 Me |
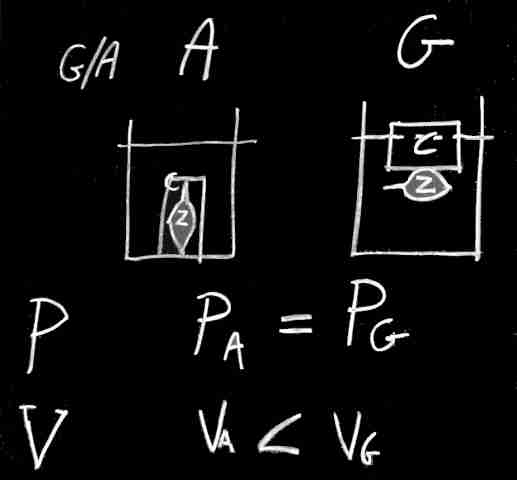
 1 Le cause del G/A sono: peso e volume del corpo.
Galleggiamento con zavorra interna o
esterna al contenitore. 2
Rapporto; tipi.
3 Densita'
di massa media di un corpo. e c: Corpi
multipli in massa e volume; unita' didattica. 1 Le cause del G/A sono: peso e volume del corpo.
Galleggiamento con zavorra interna o
esterna al contenitore. 2
Rapporto; tipi.
3 Densita'
di massa media di un corpo. e c: Corpi
multipli in massa e volume; unita' didattica. |
||||||||||||||||||||||||
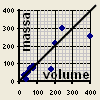
| 10 V |
Tabella della densita' delle sostanze; legno e alluminio dette in classe, da completare a casa. | Lunghezza, area e volume per il segmento, quadrato, cubo. | Retta del legno e dell'alluminio nel piano (V;M). | ||||||||||||||||||||||||
| 05 | ^^ Ottobre 2 Lab 1 2007. | ||||||||||||||||||||||||
| 13 | Lab: In classe: crz compito "corpi multipli, retta del legno e dell'alluminio". Ecz usato anche per imparare a fare i grafici cartesiani. | Formula di definizione della densita' d=M/V, formule inverse. | ||||||||||||||||||||||||
| 15 | Come disegnare la scala per l'asse cartesiano. Come disegnare il piano cartesiano (V;M). | ||||||||||||||||||||||||
| 17 | Ripasso. | ||||||||||||||||||||||||
| 06 | ^^ Ottobre 3 Lab 1 2007. | ||||||||||||||||||||||||
| 20 |
 Lab: Densita' dei corpi e delle sostanze. Densita' del sale e dello
zucchero, misurati a partire da un pacco da 1 kg acquistato da un negozio di
alimentari. Misura del volume approssimando contenuto e contenitore a un
parallelepipedo. | Misura del volume del cilindro graduato da 250 e da 1000
cm3 della beuta da 250 cm3 schematizzata come tronco
di cono. Lab: Densita' dei corpi e delle sostanze. Densita' del sale e dello
zucchero, misurati a partire da un pacco da 1 kg acquistato da un negozio di
alimentari. Misura del volume approssimando contenuto e contenitore a un
parallelepipedo. | Misura del volume del cilindro graduato da 250 e da 1000
cm3 della beuta da 250 cm3 schematizzata come tronco
di cono. |
||||||||||||||||||||||||
| 22 |
e vale anche per qualsiasi moltiplicazione es: per 2 o per 20. Compito speciale per Del Moretto. 5 Conclusione: i punti che stanno sopra la retta dell'acqua, rappresentano corpi che affondano. |
||||||||||||||||||||||||
| 24 | Occa assente legge 104/92 | ||||||||||||||||||||||||
| 07 | ^^ Ottobre 4 Lab 1 2007. | ||||||||||||||||||||||||
| 27 | Occa assente legge 104/92 | ||||||||||||||||||||||||
| 29 | ? | ||||||||||||||||||||||||
| 31 | ?Messa a punto delle valutazioni interperiodali. | ||||||||||||||||||||||||
| 08 | ^^ Novembre 1 Lab 1 2007. | ||||||||||||||||||||||||
| 03 |
|
||||||||||||||||||||||||
| 05 | ?? Scheda su ... | Cosa scrivere nella relazione? In generale gli aspetti essenziali, in questo caso: 1: piu' il volume immerso aumenta, piu' la forza di Archimede aumenta. Disegno a 2 stati di immersione e di forza. 2: Le grandezze da misurare sono 2: non solo il volume, ma anche la forza, che devono essere corrispondenti | | ||||||||||||||||||||||||
| 07 | Andamento di una corrispondenza, livello e pendenza. | Il grafico della forza di Archimede in funzione del volume immerso: rettilineo passante per l'origine. E' il grafico della diretta proporzionalita'. | ||||||||||||||||||||||||
| 09 | ^^ Novembre 2 Lab 1 2007. | ||||||||||||||||||||||||
| 10 | I vettori devono essere identificati, Es: per distinguere tra forze e
spostamenti | Condizione di
equilibrio del corpo immerso (del corpo e del sistema di forze) P+A+S=0.
| I numeri della scala e le coordinate dei punti devono stare in 2 colonne o
righe diverse |
Immergere un corpo appeso a un dinamometro. Dinamometro in acqua. Misurare la forza di Archimede. Tb:
|
||||||||||||||||||||||||
| 12 | La relaz deve essere fatta tutte le volte che si va in lab | Le forze del galleggiamento. | Condizione di equilibrio del corpo immerso (del corpo e del sistema di forze) P+A+S=0. | Sostenere, sostegno, forza di sostegno, sistema di forze di sostegno. | Sostegno, formula delle forze. | Come fare il grafico elaborazione dati "Immergere un corpo appeso a un dinamometro." | 1kgp = 9,81 N =circa 10 N | ||||||||||||||||||||||||
| 14 | no lesson | ||||||||||||||||||||||||
| 10 | ^^ Novembre 3 Lab 1 2007. | ||||||||||||||||||||||||
| 17 |
 Lab. composizione di molle. 13 presenti. |
Corpi e
deformazioni: corpo rigido, deformabile, elastico, plastico, viscoelastico,
incomprimibile, inestensibile. |
Fest => DL => Fela | Lab. composizione di molle. 13 presenti. |
Corpi e
deformazioni: corpo rigido, deformabile, elastico, plastico, viscoelastico,
incomprimibile, inestensibile. |
Fest => DL => Fela | |
||||||||||||||||||||||||
| 19 | Rivisti e presentati agli assenti le composizioni di molle fatte in lab. | Estensore a 5 molle. Condizione di equilibrio scritta coi numeri relativi. | ||||||||||||||||||||||||
| 21 | Come fare tabella e grafico per la forza elastica in funzione dell'allungamento. | ||||||||||||||||||||||||
| 11 | ^^ Novembre 4 Lab 1 2007. | ||||||||||||||||||||||||
| 24 | Scala lineare e non lineare. Scala logaritmica. | Rapporto di scala, fattore di scala. | I numeri del primo centimetro, millimetro per millimetro. | Tb per la relazione. Tb: (x;F; approssimazioni alla scala; posizioni sulla scala in cm). | Lab: misure forza elastica in funzione dell'allungamento. | ||||||||||||||||||||||||
| 26 | 1 Suddivisione del libro e sigla per indicare la lezione da studiare. 2 Corpo in equilibrio = fermo = la posizione non cambia al passare del tempo. 3 I 4 tipi di posizione. 4 U4L1 par 1,2,3 pag 102-3; U3L3 par 1,2,3,4,5,6 pag. 76 | ||||||||||||||||||||||||
| 28 | Procedimento per indagare scientificamente una corrispondenza. 1 Individuare le grandezze variabili corrispondenti Es: Forza e allungamento della molla 2 Misurare la corrispondenza e raccogliere i dati nella tb di corrispondenza 3 Grafico cartesiano della corrispondenza. 4 Dal grafico ricavare la formula. Def di allungamento di una molla in senso specifico. c: mem allungamento, Procedimento per indagare scientificamente una corrispondenza., Calibrare. |
||||||||||||||||||||||||
| 12 | ^^ Dicembre 1 Lab 1 2007. | ||||||||||||||||||||||||
| 01 |
 Lab:
Catena di cause-effetti: f esterna => allungamento => f elastica. |
Allungamento di una
molla in senso specifico. |
Asta millimetrata,
centimetrata, con becchi. |
Tabella per la presa dei dati | Tb per la
elaborazione dei dati |
Precisione grafica; calcolo dei dati grafici dai dati reali. Per assegnare
il numero al giusto millimetro. Lab:
Catena di cause-effetti: f esterna => allungamento => f elastica. |
Allungamento di una
molla in senso specifico. |
Asta millimetrata,
centimetrata, con becchi. |
Tabella per la presa dei dati | Tb per la
elaborazione dei dati |
Precisione grafica; calcolo dei dati grafici dai dati reali. Per assegnare
il numero al giusto millimetro. |
||||||||||||||||||||||||
| 03 | ?? | ||||||||||||||||||||||||
| 05 | Forza elastica, Forza esterna, Fela = - Fest es: 5=-(-5) | ||||||||||||||||||||||||
| 0812 8 dicembre Festa della Madonna | |||||||||||||||||||||||||
| 13 | ^^ Dicembre 2 Lab 1 2007. | ||||||||||||||||||||||||
| 08 | 0812 8 dicembre festa Immacolata Concezione | ||||||||||||||||||||||||
| 10 | Crz grafici delle molle | Approssimazione per difetto, eccesso, arrotondamento; all'ultima cifra, al multiplo. | Crz compito n. 3 della scheda. | | ||||||||||||||||||||||||
| 12 | Retta interpolatrice passante per l'origine. Bisettrice del settore angolare. | ||||||||||||||||||||||||
| 14 | ^^ Dicembre 3 Lab 1 2007. | ||||||||||||||||||||||||
| 15 | |
||||||||||||||||||||||||
| 17 | no lesson | ||||||||||||||||||||||||
| 19 | Calcolo retta interpolatrice per la funzione dell'attrito in funzione della forza normale, col metodo del punto medio. | ||||||||||||||||||||||||
| 15 | ^^ Gennaio 1 Happy new year ! Lab 1 2007. | ||||||||||||||||||||||||
| 7 | 1
Forza di
primo distacco. 2
Coefficiente
di attrito statico. 3
Forze concentrate
e forze distribuite.. 4
Verso della forza
peso confrontato col verso del moto. e
Rotola rettangolo su linea retta. | Rotola rettangolo su rettangolo. |
||||||||||||||||||||||||
| 9 | 1 Spostamento di un corpo. | Lo spostamento di 1 giro rotolato e' uguale al perimetro. 2 Spostamento di un corpo traslato, non ruotato. 3 c: Cfr avanzamento squadra vs registro. Grafico spostamento in funzione giri. | ||||||||||||||||||||||||
| 16 | ^^ Gennaio 2 Lab 1 2007. | ||||||||||||||||||||||||
| 12 | occa assente 104/92. | ||||||||||||||||||||||||
| 14 | 1 Rotola rettangolo su rettangolo. | ||||||||||||||||||||||||
| 16 | 1 S1G=P lo spostamento di 1 giro su una retta e' uguale al perimetro. 2 Spostamento traslatorio di un corpo rigido. | ||||||||||||||||||||||||
| 17 | ^^ Gennaio 3 Lab 1 2007. | ||||||||||||||||||||||||
| 19 |
 3
forze in equilibrio su un corpo esteso. 3
forze in equilibrio su un corpo esteso. |
||||||||||||||||||||||||
| 21 | 1 Rappresentare le forze tramite retta di applicazione, verso e intensita'. | ||||||||||||||||||||||||
| 23 | 1 Forza. Componente orizzontale e verticale. Scomposizione cartesiana, componenti cartesiane. 2 3 forze in equilibrio. Rappresentare la forza con un vettore freccia. | Scomposizione di 3 forze equilibrate. | ||||||||||||||||||||||||
| 18 | ^^ Gennaio 4 Lab 1 2007. | ||||||||||||||||||||||||
| 26 |
 In classe: rotola rett su rett 6x4 su 14x6. Dis, tb pos spost. esp: Misurare 3 forze applicate a un ometto appendiabiti. c: E' stata consegnata una scheda col disegno in scala delle forze, da scomporre. |
||||||||||||||||||||||||
| 28 | Occa assente legge 104/92 | ||||||||||||||||||||||||
| 30 | Occa assente legge 104/92. | ||||||||||||||||||||||||
| 19 | ^^ Febbraio 1 Lab 1 2007. | ||||||||||||||||||||||||
| 02 |
 1
crz Rotola rettangolo su rettangolo. 2
I segni delle coordinate cartesiane e la loro regola di rotazione.. 3
I segni degli spostamenti. 4 LAB: bottiglia forata
da 2 litri, tra-vasa in bottiglia da 0,5 litri. Misurare durata travaso per
3 riempimenti consecutivi. Precisione al secondo. Portare materiale esp a
scuola. Ripetere con approssimazione entro il 10%. e
c: Dis e Tb Posizioni e spostamenti di "rotola rettangolo su rettangolo 6x4 su 18x2". 1
crz Rotola rettangolo su rettangolo. 2
I segni delle coordinate cartesiane e la loro regola di rotazione.. 3
I segni degli spostamenti. 4 LAB: bottiglia forata
da 2 litri, tra-vasa in bottiglia da 0,5 litri. Misurare durata travaso per
3 riempimenti consecutivi. Precisione al secondo. Portare materiale esp a
scuola. Ripetere con approssimazione entro il 10%. e
c: Dis e Tb Posizioni e spostamenti di "rotola rettangolo su rettangolo 6x4 su 18x2". |
||||||||||||||||||||||||
| 04 | Occa assente, per morte zio Remo. | ||||||||||||||||||||||||
| 06 | Occa assente. | ||||||||||||||||||||||||
| 20 | ^^ Febbraio 2 Lab 1 2007. | ||||||||||||||||||||||||
| 09 | 1 I punti per la relazione di laboratorio. 2 Spiegazione esp gittata in funzione dell'altezza dell'acqua sopra il foro, e intensita' di corrente; il tutto in stato stazionario. | ||||||||||||||||||||||||
| 11 | 1 Rappresentare svuotamento e riempimento. Travaso guardato per fasi 2 c: misurare lo svuotamento di 0,5 litri, e la sua durata; da 1,5 litri | ||||||||||||||||||||||||
| 13 | 1 Come misurare tenendo conto dello spessore delle tacche del righello. | ||||||||||||||||||||||||
| 21 | ^^ Febbraio 3 Lab 1 2007. | ||||||||||||||||||||||||
| 16 | Occa assente e Renato assente. | ||||||||||||||||||||||||
| 18 | 1 Fattore di variazione. 2 La pressione. Def nel SI. | ||||||||||||||||||||||||
| 20 | 1 Fattore di aggiustamento; addendo di aggiustamento. 2 P=mg. 3 U1L3. Peso e massa pag. 72 | ||||||||||||||||||||||||
| 22 | ^^ Febbraio 4 Lab 1 2007. | ||||||||||||||||||||||||
| 23 | Occa assente, permesso legge 104/92. | ||||||||||||||||||||||||
| 25 | 1 Per confrontare 2 numeri: differenza, rapporto, differenza percentuale. | ||||||||||||||||||||||||
| 27 | 1 Verifica relazione casa+lab getto in fase stazionaria. 2 Spiega come fare esp getto svuotamento, e 2: rifare esp getto in fase stazionaria con h di un caso = 4 volte h dell'altro Es: 3 cm e 12 cm. | ||||||||||||||||||||||||
| 23 | ^^ Marzo 1 Lab 1 2007. | ||||||||||||||||||||||||
| 2 | Occa assente, permesso legge 104/92 | ||||||||||||||||||||||||
| 4 | 1 Descrizione dell'esp "getto d'acqua laterale di una bottiglia bucata" | ||||||||||||||||||||||||
| 6 | Ripasso. | ||||||||||||||||||||||||
| 24 | ^^ Marzo 2 | ||||||||||||||||||||||||
| 9 | Occa assente, legge 104/92. 1 Grafico cartesiano getto d'acqua da pressione idrostatica. Fatto come seduta di laboratorio del 9mar. | ||||||||||||||||||||||||
| 11 | 1 Disegnare in scala 1:3 il getto di uscita laterale della bottiglia. 1° passo: tabella di corrispondenza tra valori reali e in scala. 2 Grafico cartesiano della cr2var L=f(h). | ||||||||||||||||||||||||
| 13 | 1 c: Disegnare in scala 1:3 il getto di uscita laterale dalla bottiglia. 2 Esempi di calcolo della velocita'. | ||||||||||||||||||||||||
| 25 | ^^ Marzo 3 | ||||||||||||||||||||||||
| 16 |
 Occa assente, permesso legge 104/92
Occa assente, permesso legge 104/92 |
||||||||||||||||||||||||
| 18 | 1 Definizione di velocita'. 2 Esempi di calcolo. | ||||||||||||||||||||||||
| 20 | Correzione grafico cartesiano. | ||||||||||||||||||||||||
| 26 | ^^ Marzo 4 | ||||||||||||||||||||||||
| 23 |  Tratto cronometrato tramite coppia di fotocellule.
Tratto cronometrato tramite coppia di fotocellule. |
||||||||||||||||||||||||
| 25 | 1 Disegno delle oscillazioni rettilinee del pendolo. 2 Def piccole oscillaz. A=(1/10)R 3 Concezione delle forze: Aristotele vs Galileo. | ||||||||||||||||||||||||
| 27 | 1 Verifica costruzione pendoli. 2 Tipi di corpo. | ||||||||||||||||||||||||
| 27 | ^^ Marzo 5 | ||||||||||||||||||||||||
| 30 | Lab. Verifica compito: misura periodo oscillazioni pendolo di diverse lunghezze. | ||||||||||||||||||||||||
| 01 | 1 Pendoli che oscillano contemporaneamente, regolati per la stessa frequenza. 2 esp: Quando uno ha fatto 20 oscillazioni, l'altro ne ha fatto 19. 3 . 4 . 5 . 6 . e . e . | ||||||||||||||||||||||||
| 03 | 1 Fenomeno ciclico uniforme/n. 2 Numero di cicli, durata, Periodo, frequenza. 3 Teo: fT=1. 4 p: Oscillazioni di 2 pendoli: 20 e 21 cicli nella stessa durata. Calc il rapporto tra i periodi. | ||||||||||||||||||||||||
| 28 | ^^ Aprile 1 | ||||||||||||||||||||||||
| 06 |
|
||||||||||||||||||||||||
| 08 | Pasqua Mer 8 Mar 14 | ||||||||||||||||||||||||
| 10 | Pasqua | ||||||||||||||||||||||||
| 29 | ^^ Aprile 2 | ||||||||||||||||||||||||
| 13 | Pasqua | ||||||||||||||||||||||||
| 15 | 1 Gittata in funzione dell'altezza della discesa. 2 Posizione della sfera sulla linea di start. | ||||||||||||||||||||||||
| 17 | 1 Piccole oscillazioni ellittiche del pendolo. 2 d: Periodo dell'oscillazione ellittica e lineare, sono uguali? o diverse? . 3 c: Disegnare la traiettoria ellittica. | ||||||||||||||||||||||||
| 30 | ^^ Aprile 3 | ||||||||||||||||||||||||
| 20 | Siringa. Struttura. | Spiegazione su come svolgere l'esperimento: "Tirare il pistone della siringa a tenuta stagna. Misurare la forza in funzione del volume della camera."| Inizio esperimento. | ||||||||||||||||||||||||
| 22 | 1 Terminologia molla. Capo, o estremo: fisso, mobile. 2 ix Ampiezza lineare e angolare. | ||||||||||||||||||||||||
| 24 | Occa assente. Visita dottore alla mamma. | ||||||||||||||||||||||||
| 25 | Festa 25 aprile | ||||||||||||||||||||||||
| 31 | ^^ Aprile 4 | ||||||||||||||||||||||||
| 27 |
 Goniometro;
misurare un angolo con il goniometro nel caso piu' semplice di vertice e lati
accedibili. Goniometro;
misurare un angolo con il goniometro nel caso piu' semplice di vertice e lati
accedibili.1 Pompa a vuoto, campana a vuoto. 2 Confronto tra siringhe con beccuccio sigillato. 3 Tirare il pistone della siringa a tenuta stagna. Misurare la forza in funzione del volume della camera. |
||||||||||||||||||||||||
| 29 | 1 crz triangoli oscillazione pendolo. 2 c: Dis triang rettang base fissa 16 cm, passo verticale 1,6 cm, 10 passi. Misura angoli, organizza tb. 3 Spiega esperienza "Tirare il pistone della siringa a tenuta stagna". Idee per spiegare: 1: Aria dentro e fuori la siringa; 2: aria non puo' tirare, solo spingere. 4 Densita' dell'aria d=M/V, per spiegare rifacciamoci alla densita'.' 5 c: Rappresentaz densita' aria nella siringa a diversi volumi: quadrato 6x6, 2 puntini ogni quadrato; compresso a rettangolo 3x6, espanso a rettangolo 12x6. | ||||||||||||||||||||||||
| 1° Maggio festa dei lavoratori | |||||||||||||||||||||||||
| 32 | ^^ Maggio 1 | ||||||||||||||||||||||||
| 4 | Lab: Equilibrio di pesi su un'asta. 1 Spiego l'equilibrio del triangolo poggiato sulla mediana. 2 Calcolo geometrico dell'area delle 2 parti del triangolo equilatero in equilibrio sull'asta.3 Equilibrio asta soggetta a 3 forze parallele, perpendicolari all'asta. e c: Equilibrio asta soggetta a 3 forze parallele, perpendicolari all'asta. e Misurare gli angoli dei triangoli costruiti per l'appoggio sulla mediana. | ||||||||||||||||||||||||
| 6 | 1 Caso di equilibrio presentato da Grassi. 2 Idea di Archimede per spiegare la regola di equilibrio della leva. 3 Definizione di momento torcente di una forza. | ||||||||||||||||||||||||
| 8 | 1 Spiego l'equilibrio del triangolo poggiato sulla mediana. 2 Calc torcente 3 forze parallele. 3 p: Calc geometrico dell'area delle 2 parti del triangolo equilatero in equilibrio sull'asta. 4 c: Misurare gli angoli della famiglia di triangoli costruita. | ||||||||||||||||||||||||
| 33 | ^^ Maggio 2 | ||||||||||||||||||||||||
| 11 |
 |
||||||||||||||||||||||||
| 13 | 1 Elaboraz dati esperimenti. | ||||||||||||||||||||||||
| 15 | Settimana alternativa: vedevano film | ||||||||||||||||||||||||
| 34 | ^^ Maggio 3 | ||||||||||||||||||||||||
| 18 | Lab: recupero esperienze saltate. | ||||||||||||||||||||||||
| 20 | Verifica e recupero. | ||||||||||||||||||||||||
| 22 | Verifiche e recupero. | ||||||||||||||||||||||||
| 35 | ^^ Maggio 4 | ||||||||||||||||||||||||
| 25 |
 1
Spiega:scomposizione forze in componente orizzontale H e verticale V. 2
Lab: 3
forze parallele su un corpo esteso. Rifatta con punti di applicazione
piu' distanti. 1
Spiega:scomposizione forze in componente orizzontale H e verticale V. 2
Lab: 3
forze parallele su un corpo esteso. Rifatta con punti di applicazione
piu' distanti. |
||||||||||||||||||||||||
| 27 | 1 Verifiche e recupero. 2 Scritti i dati per 2 relazioni: 1: getto da pressione idrostatica Lfh; 2: svuotamento Vft 3 Verifica: scomposizione forze in componente orizzontale H e verticale V. | ||||||||||||||||||||||||
| 29 | 1 Verifica e recupero. | ||||||||||||||||||||||||
| 36 | ^^ Giugno 1 | ||||||||||||||||||||||||
| 3 | Recupero e verifiche. | ||||||||||||||||||||||||
| 5 | Recupero e verifiche. | ||||||||||||||||||||||||
| 8 | Recupero e verfiche. | ||||||||||||||||||||||||
| 10 | Recupero e verifiche. | ||||||||||||||||||||||||
| 12 | Recupero e verifiche. |